03 . série de fourier
CHOISIR
0 chapitre
04 . terminale expert
CHOISIR
0 chapitre
05 . term (STI2D/STL)
CHOISIR
0 chapitre
06 . term (STI2D/STL) spécialité
CHOISIR
0 chapitre
08 . définition
CHOISIR
0 chapitre
09 . flashmaths
CHOISIR
0 chapitre
10 . Primitive
Dans ce chapitre, nous allons faire le lien entre dérivées et primitives. Pour être à l'aise, vous devez maîtriser le chapitre : dérivation.
CHOISIR
0 chapitre
11 . Le plan et les nombres
CHOISIR
0 chapitre
12 . Voca. (1er ordre)
Dans cette partie, nous apprendrons à résoudre les équations différentielles du 1er ordre sans ou avec un second membre à coefficients constants. Puis, nous ajouterons une condition initiale. Pour être à l'aise sur cette partie, vous devez bien connaître les chapitres sur les : PRIMITIVES, ainsi que le chapitre : IDENTIFICATION.
CHOISIR
0 chapitre
13 . Voca (2nd ordre)
Dans cette partie, nous apprendrons à résoudre les équations différentielles du second ordre sans ou avec un second membre. Puis, nous ajouterons deux conditions initiales. Pour être à l'aise sur cette partie, vous devez bien connaître les chapitres : polynôme du second degré, généralités pour les complexes, IDENTIFICATION.
CHOISIR
0 chapitre
14 . Configuration du plan
CHOISIR
0 chapitre
16 . Vocabulaire
Vous trouverez des explications sur le vocabulaire, les symboles, la manière de dénombrer pour pouvoir faire des probabilités.
CHOISIR
0 chapitre
17 . Identités remarquables
Dans cette partie, les identités remarquables vous sont expliquées de manière géométrique. Puis, elles sont appliquées sur divers exemples afin de développer ou factoriser une expression.
CHOISIR
0 chapitre
19 . Le calcul intégral
Dans cette section, nous allons aborder la notion de primitives et d'intégrales. Puis, nous montrerons comment graphiquement on peut interpréter la notion d'intégrale. Pour être à l'aise avec ces nouvelles notions, vous devez être à l'aise sur le chapitre des dérivées.
CHOISIR
7 chapitres
20 . Statistiques
CHOISIR
0 chapitre
22 . Plan et les nombres
CHOISIR
0 chapitre
23 . Fonction en escalier
CHOISIR
0 chapitre
24 . dérivation, somme, produit, quotient
CHOISIR
0 chapitre
25 . Primitives
Dans cette partie, nous allons aborder les primitives et les formules pour les obtenir. Pour être à l'aise, vous devez maîtriser le chapitre sur les dérivées.
CHOISIR
0 chapitre
26 . Vocabulaire (1er ordre)
Dans cette partie, nous apprendrons à résoudre les équations différentielles du 1er ordre sans ou avec un second membre. Puis, nous ajouterons une condition initiale. Pour être à l'aise sur cette partie, vous devez bien connaître les chapitres sur les : PRIMITIVES, ainsi que le chapitre : IDENTIFICATION.
CHOISIR
0 chapitre
27 . Vocabulaire (2nd ordre)
CHOISIR
0 chapitre
28 . Les configurations du plan
CHOISIR
0 chapitre
30 . Dérivation et somme, produit, quotient
CHOISIR
0 chapitre
32 . Le principe
Dans cette partie, nous allons voir quel est l'intérêt des maps, comment les construire.
CHOISIR
0 chapitre
33 . Fonctions cos et sin
CHOISIR
0 chapitre
34 . Les primitives
CHOISIR
0 chapitre
35 . Le vocabulaire
CHOISIR
0 chapitre
36 . Voca
CHOISIR
0 chapitre
37 . Le voca
CHOISIR
0 chapitre
38 . Vocab
CHOISIR
0 chapitre
39 . suites explicites
CHOISIR
0 chapitre
40 . suites explicites (bts)
CHOISIR
0 chapitre
41 . suites explicites (1ière)
CHOISIR
0 chapitre
42 . suites explicites (term)
CHOISIR
0 chapitre
43 . Vocabulaire des matrices
CHOISIR
0 chapitre
44 . Le Vocabulaire pour les matrices
CHOISIR
0 chapitre
45 . dl et généralités
CHOISIR
0 chapitre
46 . généralités et dl
CHOISIR
0 chapitre
47 . Vocabulaire et notation
CHOISIR
0 chapitre
48 . Notation et vocabulaire
CHOISIR
0 chapitre
49 . rappel : cos et sin
CHOISIR
0 chapitre
50 . rappel sur cos et sin
CHOISIR
0 chapitre
51 . rappel : réduction au même dénominateur
CHOISIR
0 chapitre
52 . rappel sur réduire au même dénominateur
CHOISIR
0 chapitre
53 . première identité
CHOISIR
0 chapitre
56 . Famille de x
CHOISIR
0 chapitre
57 . la famille de x
CHOISIR
0 chapitre
58 . la formule k(a+b) = ka+kb
CHOISIR
0 chapitre
59 . Formule : k(a+b) =ka+kb
CHOISIR
0 chapitre
60 . distribuer avec k(a+b)
CHOISIR
0 chapitre
61 . Définition et vocabulaire
CHOISIR
0 chapitre
62 . Définition d'une fraction
CHOISIR
0 chapitre
63 . Vocabulaire pour les fractions
CHOISIR
0 chapitre
64 . Comprendre la notion de fraction
CHOISIR
0 chapitre
65 . La première : (a+b)^2 = ...
CHOISIR
0 chapitre
66 . Vocabulaire et matrices
CHOISIR
0 chapitre
67 . Pré requis : développer
CHOISIR
0 chapitre
68 . Outils pour résoudre : développer
CHOISIR
0 chapitre
69 . le schéma de Bernouilli
CHOISIR
0 chapitre
70 . Expérience de Bernouilli
CHOISIR
0 chapitre
71 . pédagogie
CHOISIR
0 chapitre
73 . Composition
CHOISIR
0 chapitre
74 . affine (term)
CHOISIR
0 chapitre
75 . affine (1ere)
CHOISIR
0 chapitre
76 . et le produit
CHOISIR
0 chapitre
77 . d'un produit
CHOISIR
0 chapitre
79 . Factoriser/ Développer (1ère)
CHOISIR
0 chapitre
81 . Factoriser/ Développer (term)
CHOISIR
0 chapitre
83 . Prérequis : résolution de systèmes
CHOISIR
0 chapitre
84 . Prérequis : résoudre des systèmes
CHOISIR
0 chapitre
85 . Définition et tracer
CHOISIR
0 chapitre
86 . prérequis : forme exponentielle d'un complexe
CHOISIR
0 chapitre
87 . rappel : forme exponentielle d'un complexe
CHOISIR
0 chapitre
88 . Pré requis : la fonction échelon unité
CHOISIR
0 chapitre
89 . Pré requis : fct échelon unité
CHOISIR
0 chapitre
90 . complexes : tout ce qu'il faut savoir
CHOISIR
0 chapitre
91 . complexes : tout ce qu'il faut savoir
CHOISIR
0 chapitre
92 . cplx : tout ce qu'il faut savoir
CHOISIR
0 chapitre
93 . cplx: tout ce qu'il faut savoir
CHOISIR
0 chapitre
94 . tout ce qu'il faut retenir
CHOISIR
0 chapitre
95 . tout ce qu'il faut retenir
CHOISIR
0 chapitre
96 . tout ce qu'il faut retenir
CHOISIR
0 chapitre
97 . tout ce qu'il faut retenir
CHOISIR
0 chapitre
98 . tout ce qu'il faut retenir
CHOISIR
0 chapitre
99 . Définition d'une fonction
CHOISIR
0 chapitre
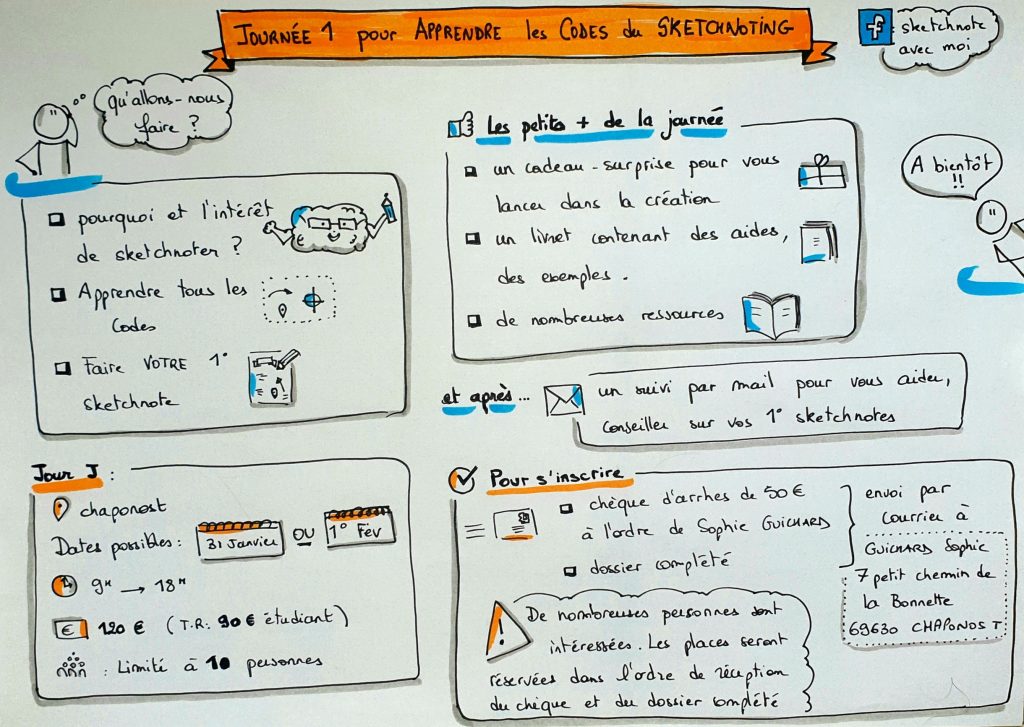
100 . Sketchnoting

Deux dates clés pour une journée de formation
pour apprendre tous les codes à 20 minutes de Lyon !!
Soit le vendredi 31 Janvier Soit le samedi 1er Février 2020.
pour plus d'informations cliquez ici...
En tout cas, les cartes mentales font partie des structures du sketchnoting. Donc si vous faites des cartes mentales, vous faites déjà du sketchnoting !!! Mais il existe d'autres structures qui vont vous permettre de contextualiser, de gagner en liberté de présentation, de création. Tout cela se réalise à partir de divers codes et de pictogrammes...CHOISIR
3 chapitres
101 . ... des pictos
CHOISIR
0 chapitre
104 . partie 1
CHOISIR
0 chapitre
105 . proba. conditionnelles
CHOISIR
0 chapitre
106 . original
CHOISIR
0 chapitre
107 . forme trigonométrique
CHOISIR
0 chapitre
108 . avec de la nourriture
CHOISIR
0 chapitre
110 . avec des points alignés
CHOISIR
0 chapitre
111 . étoile à 8 branches
CHOISIR
0 chapitre
112 . sur un quart
CHOISIR
0 chapitre
113 . inverse
CHOISIR
0 chapitre
114 . à 6 branches
CHOISIR
0 chapitre
115 . avec la nature autour de soi
CHOISIR
0 chapitre
116 . intro
CHOISIR
0 chapitre
117 . Formule de BEssel
CHOISIR
0 chapitre
118 . polynômes et identification
CHOISIR
0 chapitre
119 . DérivéeS
CHOISIR
0 chapitre
121 . Généralités
Dans cette section, nous allons découvrir qui sont les complexes et comment faire du calcul avec ces nouveaux nombres. Nous parlerons de la première forme des nombres complexes : la forme algébrique.
CHOISIR
0 chapitre
123 . généralités fct
CHOISIR
0 chapitre
124 . Vecteurs et le plan
CHOISIR
0 chapitre
125 . Second degré
CHOISIR
0 chapitre
127 . Géométriques
CHOISIR
0 chapitre
128 . Les généralités
Dans cette section, nous allons découvrir qui sont les complexes et comment faire du calcul avec ces nouveaux nombres. Nous parlerons de la première forme des nombres complexes : la forme algébrique.
CHOISIR
0 chapitre
129 . Loi binomiale (déf et prop)
Dans cette section, nous allons caractériser la loi binomiale. Nous verrons comment calculer son espérance, son écart-type ainsi que la formule du calcul des probabilités. Enfin, nous ferons des exercices afin de mettre tout cela en pratique.
CHOISIR
0 chapitre
130 . en escalier
CHOISIR
0 chapitre
131 . parité
CHOISIR
0 chapitre
132 . Factoriser / développer
CHOISIR
0 chapitre
136 . Principe de base
CHOISIR
0 chapitre
138 . Les Equations de droites
CHOISIR
0 chapitre
139 . Forme algébrique
CHOISIR
0 chapitre
140 . Probabilités de base
CHOISIR
0 chapitre
141 . proba discrète : loi binomiale (déf et prop.)
CHOISIR
0 chapitre
142 . série arithmétique
CHOISIR
0 chapitre
143 . Généralités sur C
CHOISIR
0 chapitre
144 . Théorie de base
CHOISIR
0 chapitre
145 . La théorie
CHOISIR
0 chapitre
147 . Exemples
Dans cette partie, nous allons découvrir différents types de maps que vous pourrez télécharger. Pensez à partager vos maps elles seront stockées avec cette vidéo!
CHOISIR
0 chapitre
148 . Nombres complexes
CHOISIR
0 chapitre
149 . Intégrale
Dans cette partie, nous allons définir les intégrales et les différentes techniques de calcul. Pour être à l'aise, vous devez bien connaître le chapitre sur les primitives.
CHOISIR
0 chapitre
150 . Intégrales
Dans cette partie, nous allons définir les intégrales et les différentes techniques de calcul. Pour être à l'aise, vous devez bien connaître le chapitre sur les primitives.
CHOISIR
0 chapitre
151 . Les intégrales
CHOISIR
0 chapitre
153 . Le calcul de proba
CHOISIR
0 chapitre
154 . Calcul de proba
CHOISIR
0 chapitre
155 . Théorie (1er ordre)
CHOISIR
0 chapitre
156 . La théorie (1er ordre)
CHOISIR
0 chapitre
157 . arithmétiques (1ière)
CHOISIR
0 chapitre
158 . dl et opérations
CHOISIR
0 chapitre
159 . opérations et dl
CHOISIR
0 chapitre
160 . suites récurrentes (bts)
CHOISIR
0 chapitre
161 . suites récurrentes (Term)
CHOISIR
0 chapitre
162 . suites récurrentes
CHOISIR
0 chapitre
164 . rappel sur l'intégration par partie
CHOISIR
0 chapitre
165 . rappel : intégration par partie
CHOISIR
0 chapitre
166 . rappel : identification
CHOISIR
0 chapitre
167 . rappel sur l'identification
CHOISIR
0 chapitre
168 . Fonction échelon unité
CHOISIR
0 chapitre
169 . seconde identité
CHOISIR
0 chapitre
170 . Famille de x^2
CHOISIR
0 chapitre
171 . la famille de x^2
CHOISIR
0 chapitre
174 . formule (a+b)(c+d)
CHOISIR
0 chapitre
175 . la formule (a+b)(c+d)
CHOISIR
0 chapitre
176 . double distributivité
CHOISIR
0 chapitre
177 . transformer une fraction
CHOISIR
0 chapitre
178 . comment transformer une fraction
CHOISIR
0 chapitre
179 . La seconde : (a-b)^2
CHOISIR
0 chapitre
180 . La somme de matrices
CHOISIR
0 chapitre
181 . la somme
CHOISIR
0 chapitre
182 . Somme et matrices
CHOISIR
0 chapitre
183 . Pré requis : factoriser
CHOISIR
0 chapitre
184 . Outils pour résoudre : factoriser
CHOISIR
0 chapitre
185 . Pré requis avec le dévelopement
CHOISIR
0 chapitre
186 . Pré requis : savoir développer
CHOISIR
0 chapitre
187 . Pré requis : les suites
CHOISIR
0 chapitre
188 . Pré requis : suites
CHOISIR
0 chapitre
189 . Le radian et les multiples de pi; pi/2 et pi/4
CHOISIR
0 chapitre
190 . Radian et les multiples de pi; pi/2 et pi/4
CHOISIR
0 chapitre
191 . Radian et multiples de pi; pi/2 et pi/4
CHOISIR
0 chapitre
192 . Le radian et multiples de pi; pi/2 et pi/4
CHOISIR
0 chapitre
193 . Radian et les multiples de pi ; de pi/2 et de pi/4
CHOISIR
0 chapitre
194 . La théorie (2nd ordre SANS 2nd membre)
CHOISIR
0 chapitre
195 . Théorie (2nd ordre SANS 2nd membre)
CHOISIR
0 chapitre
196 . dérivation et composition
CHOISIR
0 chapitre
197 . dérivation et composer de fonctions
CHOISIR
0 chapitre
198 . carrée
CHOISIR
0 chapitre
199 . d'un quotient
CHOISIR
0 chapitre
200 . identités remarquables (1ère)
CHOISIR
0 chapitre
201 . Identités remarquables (Term)
CHOISIR
0 chapitre
202 . et le quotient
CHOISIR
0 chapitre
204 . influence de m et p
CHOISIR
0 chapitre
205 . prérequis : le symbole sigma
CHOISIR
0 chapitre
206 . rappel : le symbole sigma
CHOISIR
0 chapitre
207 . Journée de formation pour apprendre les codes
Les premières journées de formation au sketchnoting ont eu lieu !
et ce fut un succès !
Je renouvelle cette journée 1 de formation sur deux dates
au choix : le vendredi 31 janvier ou le samedi 1er février
CHOISIR
0 chapitre
208 . cours à distance
Dans cette partie, vous trouverez de nombreux points bilan de cours, comme des synthèses. Je remettrais en dessous les playlists de vidéos correspondantes ainsi que la synthèse en image. Révisez bien. Vous pouvez pour ceux qui accompagnent les élèves suivre les articles autour de "trucs et astuces pour mettre un enseignement à distance efficace" Vous pouvez également télécharger le fichier CADEAU avec le tableau répertoriant toutes les vidéos (reliées à des qrcodes, ou des numéros) afin que vous puissiez les insérer dans vos cours.
CHOISIR
9 chapitres
209 . ln, log et exponentielle
CHOISIR
0 chapitre
210 . proba discrètes (1)
CHOISIR
0 chapitre
212 . primitives et intégrales
CHOISIR
0 chapitre
213 . partie 2
CHOISIR
0 chapitre
214 . avec des éléments de la nature
CHOISIR
0 chapitre
215 . démonstration de création
CHOISIR
0 chapitre
217 . à 12 branches
CHOISIR
0 chapitre
218 . inverse
CHOISIR
0 chapitre
220 . Intégrale et aire
CHOISIR
0 chapitre
222 . Etude qualitative
CHOISIR
0 chapitre
223 . Vecteurs dans un repère
CHOISIR
0 chapitre
224 . Résolution d'équations
CHOISIR
0 chapitre
225 . Proba. conditionnelle
Vous trouverez des cours sur la notion de probabilité conditionnelle en appui sur soit l'arbre, soit le tableau à double entrée.
CHOISIR
0 chapitre
226 . de Riemann
CHOISIR
0 chapitre
227 . Résolution d'équations sur C
CHOISIR
0 chapitre
228 . résoudre sur C
Dans cette section, nous allons résoudre des équations du 1er, 2nd et 3ième degré. Pour être à l'aise, vous devez bien connaître le chapitre : généralités pour les complexes.
CHOISIR
0 chapitre
231 . L'étude qualitative
CHOISIR
0 chapitre
232 . Fonctions affines
CHOISIR
0 chapitre
233 . Intégrales et aires
CHOISIR
0 chapitre
234 . Plan et vecteurs
CHOISIR
0 chapitre
235 . Résoudre les équations sur C
CHOISIR
0 chapitre
236 . Proba. conditionnelles
CHOISIR
0 chapitre
237 . série géométrique
CHOISIR
0 chapitre
239 . équations
CHOISIR
0 chapitre
240 . Résoudre des éq. sur C
CHOISIR
0 chapitre
241 . Probabilités conditionnelles
CHOISIR
0 chapitre
245 . Equations différentielles
Dans cette section, nous allons aborder les maps relatives aux équations différentielles du 1er et 2nd ordre à coefficients constants.
CHOISIR
0 chapitre
246 . Théorie (2nd ordre AVEC 2nd membre)
CHOISIR
0 chapitre
247 . La théorie (2nd ordre AVEC 2nd membre)
CHOISIR
0 chapitre
248 . Arithmétiques (thèmes)
CHOISIR
0 chapitre
249 . arithmétiques (bts)
CHOISIR
0 chapitre
250 . Géométriques (1ière)
CHOISIR
0 chapitre
251 . arithmétiques (term)
CHOISIR
0 chapitre
252 . rappel : intégrale, parité
CHOISIR
0 chapitre
253 . rappel sur intégrale et parité
CHOISIR
0 chapitre
254 . rappel : fonction échelon unité
CHOISIR
0 chapitre
255 . rappel sur la fonction échelon unité
CHOISIR
0 chapitre
256 . échelon unité
CHOISIR
0 chapitre
258 . troisième identité
CHOISIR
0 chapitre
259 . Simplifier une fraction
CHOISIR
0 chapitre
260 . simplifier des fractions
CHOISIR
0 chapitre
261 . Famille de x^3
CHOISIR
0 chapitre
262 . la famille de x^3
CHOISIR
0 chapitre
263 . La troisième : a^2 - b^2
CHOISIR
0 chapitre
264 . Produit d'une matrice par un réel
CHOISIR
0 chapitre
265 . le produit d'une matrice par un réel
CHOISIR
0 chapitre
266 . Produit d'une matrice par un nombre réel
CHOISIR
0 chapitre
267 . Développer des expressions
CHOISIR
0 chapitre
268 . Développer des expressions (exemples)
CHOISIR
0 chapitre
269 . S'entraîner à développer
CHOISIR
0 chapitre
271 . théorème d'identification
CHOISIR
0 chapitre
272 . le théorème d'identification
CHOISIR
0 chapitre
273 . Pré requis : les suites récurrentes
CHOISIR
0 chapitre
274 . Pré requis : suites récurrentes
CHOISIR
0 chapitre
275 . Loi binomiale (calcul de proba.)
CHOISIR
0 chapitre
276 . proba discrète : loi binomiale (calcul de proba)
CHOISIR
0 chapitre
277 . Les angles multiples de pi/3 et pi/6
CHOISIR
0 chapitre
278 . Angles multiples de pi/3 et pi/6
CHOISIR
0 chapitre
279 . Les angles multiples de pi/3 et de pi/6
CHOISIR
0 chapitre
280 . Angles multiples de pi/3 et de pi/6
CHOISIR
0 chapitre
281 . Multiples de pi/3 et pi/6
CHOISIR
0 chapitre
282 . racine carrée (term)
CHOISIR
0 chapitre
283 . au dénominateur
CHOISIR
0 chapitre
284 . au dénominateur
CHOISIR
0 chapitre
285 . périodicité
CHOISIR
0 chapitre
286 . inverse (1ère)
CHOISIR
0 chapitre
288 . Sens de variation
CHOISIR
0 chapitre
289 . Sens de variation (term)
CHOISIR
0 chapitre
290 . fractions : simplifier
CHOISIR
0 chapitre
291 . Fractions : simplifier (1ere)
CHOISIR
0 chapitre
292 . Fractions : simplifier (Term)
CHOISIR
0 chapitre
294 . prérequis : les racines n-ièmes de l'unité
CHOISIR
0 chapitre
296 . rappel : les racines n-ièmes de l'unité
CHOISIR
0 chapitre
297 . Mandalas
Je suis heureuse de vous partager cette nouvelle catégorie qui va lier les maths, la géométrie et l'art en allant explorer les mandalas !! Les vidéos proposées seront des tutos pour apprendre pas à pas. Vous pourrez télécharger - des fiches de construction, - des idées d'atelier à réaliser pour vous, avec des enfants, entre amis... - des fiches pour imprimer vos supports de fond si jamais vous n'avez pas le temps de créer la structure ou que vous continuez à faire un blocage dans le lien aux mathématiques !! NOUVEAU : un replay pour apprendre pas à faire à faire votre premier mandala. C est par ici !! Retrouvez nos offres dans la partie Boutique J ai envie de vous permettre de vous amuser en construisant pour aller vers vos propres créations avec des procédés simples, du matériel que vous avez à portée de main !!! et aussi de découvrir une autre facette des mathématiques, celle qui mène à la création, à votre créativité, à la beauté Partagez-moi vos créations sur la page Facebook Mandala du Coeur !! j ai hâte de découvrir vos merveilles, vos remarques, vos ressentis par rapport à ce nouveau projet ...
CHOISIR
7 chapitres
298 . bases de géométrie et conseils pour démarrer un mandala
CHOISIR
0 chapitre
299 . proba.continues
CHOISIR
0 chapitre
301 . défi
CHOISIR
0 chapitre
302 . à 24 branches
CHOISIR
0 chapitre
303 . tfd et fft
CHOISIR
0 chapitre
304 . Forme trigonométrique
CHOISIR
0 chapitre
305 . Dérivation et somme, produit, quotient
CHOISIR
0 chapitre
306 . Sens trigo. et les angles remarquables
CHOISIR
0 chapitre
307 . Résolution graphique
CHOISIR
0 chapitre
308 . Equations de droite
CHOISIR
0 chapitre
309 . Identités remarquables
CHOISIR
0 chapitre
311 . Sens trigo. et les angles remarquables
CHOISIR
0 chapitre
313 . La forme trigonométrique
CHOISIR
0 chapitre
315 . affines
CHOISIR
0 chapitre
317 . Sens trigo et les angles remarquables
CHOISIR
0 chapitre
318 . La résolution graphique
CHOISIR
0 chapitre
319 . carrée et Les polynômes
CHOISIR
0 chapitre
320 . Les courbes paramétrées
CHOISIR
0 chapitre
321 . repère et vecteurs
CHOISIR
0 chapitre
322 . Forme trigo.
CHOISIR
0 chapitre
323 . proba discrète : loi de Poisson
CHOISIR
0 chapitre
324 . série de Riemann
CHOISIR
0 chapitre
326 . La forme trigo.
CHOISIR
0 chapitre
327 . Sens trigo et les angles remarquables
CHOISIR
0 chapitre
328 . Intégration par partie
CHOISIR
0 chapitre
329 . IPP
CHOISIR
0 chapitre
331 . Géométriques (thèmes)
CHOISIR
0 chapitre
332 . géométriques (bts)
CHOISIR
0 chapitre
333 . Géométriques (term)
CHOISIR
0 chapitre
334 . rappel : fonction périodique
CHOISIR
0 chapitre
335 . rappel sur les fonctions périodiques
CHOISIR
0 chapitre
336 . rappel : intégrale généralisée
CHOISIR
0 chapitre
337 . les fonctions causales
CHOISIR
0 chapitre
340 . Ajouter 2 fractions : cas numérique
CHOISIR
0 chapitre
341 . addition de fractions ayant le même dénominateur
CHOISIR
0 chapitre
342 . Regrouper les éléments des différentes familles
CHOISIR
0 chapitre
343 . Comment regrouper les éléments des différentes familles
CHOISIR
0 chapitre
345 . Intégrale, parité et périodicité
CHOISIR
0 chapitre
346 . produit et matrices
CHOISIR
0 chapitre
347 . le produit
CHOISIR
0 chapitre
348 . produit et matrices
CHOISIR
0 chapitre
350 . Outils pour résoudre : simplifier une fraction
CHOISIR
0 chapitre
351 . Pré requis : simplifier une fraction
CHOISIR
0 chapitre
352 . Sauriez-vous développer (a+b)(c+d+e)?
CHOISIR
0 chapitre
353 . Développons (a+b)(c+d+e)...
CHOISIR
0 chapitre
354 . entières
CHOISIR
0 chapitre
355 . Pré requis : réduction au mm dénominateur
CHOISIR
0 chapitre
356 . pré requis : réduire au mm dénominateur
CHOISIR
0 chapitre
357 . Angles remarquables et sens trigo.
CHOISIR
0 chapitre
358 . identifier avec des fonctions rationnelles
CHOISIR
0 chapitre
359 . identification et fonction rationnelle
CHOISIR
0 chapitre
360 . racine carrée (1ere) :
CHOISIR
0 chapitre
361 . inverse (term)
CHOISIR
0 chapitre
362 . la fonction racine carrée
CHOISIR
0 chapitre
363 . Fractions : addition (1ère)
CHOISIR
0 chapitre
364 . Fractions : addition (Term)
CHOISIR
0 chapitre
366 . Tangente à la courbe
CHOISIR
0 chapitre
367 . Tangente à la courbe (Term)
CHOISIR
0 chapitre
368 . Evenements indépendants
CHOISIR
0 chapitre
369 . Evénements indépendants (term)
CHOISIR
0 chapitre
370 . Evénements indépendants (BTS)
CHOISIR
0 chapitre
371 . Blog
CHOISIR
0 chapitre
372 . prérequis : les matrices, vocabulaire
CHOISIR
0 chapitre
373 . rappel : les matrices, vocabulaire
CHOISIR
0 chapitre
374 . loi de Poisson
CHOISIR
0 chapitre
375 . apprendre à créer un mandala rythmé en 18
CHOISIR
0 chapitre
378 . fleur de vie
CHOISIR
0 chapitre
380 . Fonction affine
Dans ce chapitre, vous apprendrez la notion de fonction affine, de coefficient directeur, d'ordonnée à l'origine. Vous découvrirez comment tracer la courbe d'une fonction affine et comment vérifier que votre courbe est juste. Pour finir, vous verrez les notions de tableaux de variations et de signe.
CHOISIR
0 chapitre
381 . Géométrie dans l'espace
CHOISIR
0 chapitre
382 . Statistique
CHOISIR
0 chapitre
384 . Fonctions cos et sin
CHOISIR
0 chapitre
385 . carrée et polynômes
CHOISIR
0 chapitre
386 . les limites
CHOISIR
0 chapitre
387 . L'espace
CHOISIR
0 chapitre
388 . série à termes positifs
CHOISIR
0 chapitre
390 . Composition
CHOISIR
0 chapitre
391 . Lien avec la phys.
CHOISIR
0 chapitre
392 . Avec les limites
CHOISIR
0 chapitre
393 . Intégrale, parité
CHOISIR
0 chapitre
394 . Parité et intégrale
CHOISIR
0 chapitre
396 . rappel : intégrale et périodicité
CHOISIR
0 chapitre
397 . rappel sur intégrale et périodicité
CHOISIR
0 chapitre
398 . Fonctions causales
CHOISIR
0 chapitre
399 . La composition
CHOISIR
0 chapitre
400 . addition d'une fraction avec un entier
CHOISIR
0 chapitre
401 . Ajouter des fractions : cas algébrique
CHOISIR
0 chapitre
402 . Outils pour résoudre : Mettre au même dénominateur (calcul littéral)
CHOISIR
0 chapitre
403 . Pré requis : réduire au même dénominateur
CHOISIR
0 chapitre
404 . Fractions : multiplication
CHOISIR
0 chapitre
405 . Identifier dans d'autres circonstances
CHOISIR
0 chapitre
406 . Savoir identifier dans d'autres situations
CHOISIR
0 chapitre
409 . Pré requis : identification
CHOISIR
0 chapitre
410 . Pré requis : l'identification
CHOISIR
0 chapitre
411 . Transformée en Z.
CHOISIR
0 chapitre
412 . Schéma de Bernouilli
CHOISIR
0 chapitre
414 . Mesure principale
CHOISIR
0 chapitre
415 . La mesure principale
CHOISIR
0 chapitre
416 . Mesure principale d'un angle
CHOISIR
0 chapitre
417 . La mesure principale d'un angle
CHOISIR
0 chapitre
418 . Mesure principale d'un angle sur le cercle
CHOISIR
0 chapitre
419 . fonction inverse et rationnelle
CHOISIR
0 chapitre
420 . dérivation et composition de fonctions
CHOISIR
0 chapitre
423 . ln (term)
CHOISIR
0 chapitre
424 . Fractions : multiplication (1ère)
CHOISIR
0 chapitre
425 . Fractions : multiplier
CHOISIR
0 chapitre
427 . Propriétés sur le module et l'argument
CHOISIR
0 chapitre
428 . Prop. sur le module et l'argument (Term)
CHOISIR
0 chapitre
429 . Prop. sur le module et l'argument (BTS)
CHOISIR
0 chapitre
430 . Fraction : simplification
CHOISIR
0 chapitre
431 . inverser une matrice
CHOISIR
0 chapitre
432 . L'inverse d'une matrice
CHOISIR
0 chapitre
433 . Inverse d'une matrice
CHOISIR
0 chapitre
434 . prérequis : les matrices et les opérations
CHOISIR
0 chapitre
435 . rappel : matrices et opérations
CHOISIR
0 chapitre
436 . approximation d'une binomiale par une poisson
CHOISIR
0 chapitre
437 . approcher une loi binomiale par une loi de poisson
CHOISIR
0 chapitre
440 . Fonction carré et Polynôme du 2nd degré
CHOISIR
0 chapitre
442 . Probabilité continue
En s'appuyant sur le cas des probabilités discrètes, nous mettons en place les notions de variable aléatoire continue.
CHOISIR
0 chapitre
443 . Dériver et somme, produit, quotient
CHOISIR
0 chapitre
445 . racine carrée
CHOISIR
0 chapitre
447 . Fonctions racines carrées
CHOISIR
0 chapitre
449 . proba. continues
CHOISIR
0 chapitre
450 . série alternée
CHOISIR
0 chapitre
451 . Les puissances
CHOISIR
0 chapitre
452 . La parité
CHOISIR
0 chapitre
453 . Lien avec la physique
CHOISIR
0 chapitre
454 . Avec la physique
CHOISIR
0 chapitre
455 . Avec la phys.
CHOISIR
0 chapitre
459 . intégrale et périodicité
CHOISIR
0 chapitre
460 . périodicité et intégrale
CHOISIR
0 chapitre
461 . Développer en série de Fourier
CHOISIR
0 chapitre
462 . Développement en série de Fourier
CHOISIR
0 chapitre
463 . Définition de la TDL
CHOISIR
0 chapitre
464 . Composition
CHOISIR
0 chapitre
466 . addition de fractions avec 2 déno. différents
CHOISIR
0 chapitre
467 . cos et sin d'un angle
CHOISIR
0 chapitre
468 . cosinus et sinus d'un angle
CHOISIR
0 chapitre
469 . le cos et sin d un angle
CHOISIR
0 chapitre
470 . le cosinus et sinus d'un angle
CHOISIR
0 chapitre
471 . recherche des valeurs interdites
CHOISIR
0 chapitre
472 . Fractions : réduction au même dénominateur
CHOISIR
0 chapitre
473 . Outils pour résoudre : recherche des valeurs interdites
CHOISIR
0 chapitre
474 . Pré requis : recherche des valeurs interdites
CHOISIR
0 chapitre
475 . Fractions : inverser une fraction
CHOISIR
0 chapitre
476 . fractions
CHOISIR
0 chapitre
477 . Pré requis : la composition
CHOISIR
0 chapitre
478 . pré requis : composition
CHOISIR
0 chapitre
479 . la loi binomiale : déf et prop
CHOISIR
0 chapitre
480 . Dérivation dans d'autres situations
CHOISIR
0 chapitre
481 . exp (Term)
CHOISIR
0 chapitre
482 . Fractions : diviser (1ère)
CHOISIR
0 chapitre
483 . Fractions : inverser
CHOISIR
0 chapitre
484 . Sens de variation (BTS)
CHOISIR
0 chapitre
485 . Résoudre les systèmes linéaires
CHOISIR
0 chapitre
486 . Résolution des systèmes linéaires
CHOISIR
0 chapitre
487 . Résolution de systèmes linéaires
CHOISIR
0 chapitre
488 . prérequis : systèmes linéaires d'équations et matrices
CHOISIR
0 chapitre
489 . rappel : matrices et systèmes linéaires d'équations
CHOISIR
0 chapitre
491 . mandala éphémère
cette série d'ateliers mandalas sont des pistes à explorer avec les enfants dès 3 ans !! Pensez à nous partager vos photos sur notre page facebook : Mandala du coeur
CHOISIR
2 chapitres
492 . Forme exponentielle
CHOISIR
0 chapitre
494 . Fonction homographique
CHOISIR
0 chapitre
495 . Résolution d'inéquations
CHOISIR
0 chapitre
497 . Fonction LN
CHOISIR
0 chapitre
498 . La Forme exponentielle
CHOISIR
0 chapitre
499 . inéquations
CHOISIR
0 chapitre
500 . résoudre des équations trigo.
CHOISIR
0 chapitre
501 . résolution d'équations trigo.
CHOISIR
0 chapitre
502 . Forme exponentielle
CHOISIR
0 chapitre
503 . résoudre des équations trigonométriques
CHOISIR
0 chapitre
504 . résoudre des éq. avec du cos et sin
CHOISIR
0 chapitre
506 . rappel
CHOISIR
0 chapitre
508 . Dsf et parité
CHOISIR
0 chapitre
509 . Parité et DSF
CHOISIR
0 chapitre
510 . Intégrale généralisée
CHOISIR
0 chapitre
511 . définition et propriétés
CHOISIR
0 chapitre
512 . Propriétés de linéarité
CHOISIR
0 chapitre
513 . Exemple sur l'addition des fractions
CHOISIR
0 chapitre
514 . Multiplication de fractions
CHOISIR
0 chapitre
515 . Résoudre des ...
Dans cette partie, nous allons apprendre à résoudre différents types de structures : les équations, les inéquations puis les systèmes. Il est important pour les deux premiers éléments que vous dominiez bien la partie : FRACTIONS : réduction au même dénominateur dans le cas algébrique.
CHOISIR
8 chapitres
516 . Pré requis : Série entière
CHOISIR
0 chapitre
517 . Pré requis : Séries entières
CHOISIR
0 chapitre
518 . Les séries entières
CHOISIR
0 chapitre
519 . la loi uniforme
CHOISIR
0 chapitre
520 . Loi uniforme
CHOISIR
0 chapitre
521 . la loi binomiale : calcul de proba.
CHOISIR
0 chapitre
522 . inverse et rationnelles
CHOISIR
0 chapitre
523 . dériver avec la composition
CHOISIR
0 chapitre
524 . Fractions : diviser une fraction
CHOISIR
0 chapitre
525 . Racine carrée (1ère) : produit
CHOISIR
0 chapitre
526 . Fractions : diviser (Term)
CHOISIR
0 chapitre
527 . La périodicité
CHOISIR
0 chapitre
528 . Tangente à la courbe (BTS)
CHOISIR
0 chapitre
529 . fraction : la multiplication
CHOISIR
0 chapitre
530 . TFD : définition
CHOISIR
0 chapitre
531 . Définition de la TFD
CHOISIR
0 chapitre
534 . Calcul intégral
Dans cette section, nous allons aborder la notion de primitives et d'intégrales. Puis, nous montrerons comment graphiquement on peut interpréter la notion d'intégrale. Pour être à l'aise avec ces nouvelles notions, vous devez être à l'aise sur le chapitre des dérivées.
CHOISIR
6 chapitres
535 . Limites
CHOISIR
0 chapitre
536 . Trigonométrie
CHOISIR
0 chapitre
537 . Théorème de Dirichlet
CHOISIR
0 chapitre
538 . ln
CHOISIR
0 chapitre
540 . Le théorème de Dirichlet
CHOISIR
0 chapitre
541 . systèmes
CHOISIR
0 chapitre
542 . Fonctions cos et sin
CHOISIR
0 chapitre
543 . Transformations d'expressions avec du cos et sin
CHOISIR
0 chapitre
544 . Transformations d'expressions avec du cos et du sin
CHOISIR
0 chapitre
545 . seconde
CHOISIR
0 chapitre
547 . Propriétés : linéarité
CHOISIR
0 chapitre
548 . et la dérivée 1ière et 2nde
CHOISIR
0 chapitre
549 . Multiplier des fractions
CHOISIR
0 chapitre
550 . Inverser une fraction
CHOISIR
0 chapitre
551 . Fractions : l'inverse d'une fraction
CHOISIR
0 chapitre
552 . Signaux discrets
CHOISIR
0 chapitre
553 . les signaux discrets
CHOISIR
0 chapitre
554 . racine carrée (BTS) : produit
CHOISIR
0 chapitre
555 . Racine carrée (Term) : produit
CHOISIR
0 chapitre
556 . racine carrée (1ere) : quotient
CHOISIR
0 chapitre
557 . le sens de variation
CHOISIR
0 chapitre
558 . fonction log
CHOISIR
0 chapitre
559 . prop avec l'exponentielle
CHOISIR
0 chapitre
560 . prop. avec la forme exp
CHOISIR
0 chapitre
561 . propriétés avec la forme exp.
CHOISIR
0 chapitre
562 . la loi de Poisson
CHOISIR
0 chapitre
563 . la loi exponentielle
CHOISIR
0 chapitre
564 . loi exponentielle
CHOISIR
0 chapitre
565 . Fast Fourier Transform (fft)
CHOISIR
0 chapitre
566 . la fft (Fast Fourier Transform)
CHOISIR
0 chapitre
568 . Transformations complexes
CHOISIR
0 chapitre
571 . Loi normale
Cette section est un cas particulier de la partie : Probabilité continue. Ici, nous étudierons la loi normale en s'appuyant sur la loi normale centrée réduite N(0;1). Pour être à l'aise avec cette partie, il faut avoir acquis les cours de la section : Probabilité discrète.
CHOISIR
0 chapitre
572 . Fonction exponentielle
CHOISIR
0 chapitre
573 . les transformations complexes
CHOISIR
0 chapitre
574 . La Loi normale
CHOISIR
0 chapitre
577 . avec la dérivée 1ière et 2nde
CHOISIR
0 chapitre
579 . recherche de l'original
CHOISIR
0 chapitre
580 . l'inverse d'une fraction
CHOISIR
0 chapitre
581 . Diviser par une fraction
CHOISIR
0 chapitre
582 . signaux retardés
CHOISIR
0 chapitre
583 . les signaux retardés
CHOISIR
0 chapitre
584 . intégrales de f et f^2
CHOISIR
0 chapitre
585 . intégrales de f et de f^2
CHOISIR
0 chapitre
586 . Probas continues
CHOISIR
0 chapitre
587 . Dérivation dans d autres contextes
CHOISIR
0 chapitre
588 . racine carrée (1ere) : au dénominateur
CHOISIR
0 chapitre
589 . racine carrée (term) : quotient
CHOISIR
0 chapitre
590 . racine carrée (BTS) : quotient
CHOISIR
0 chapitre
591 . Tangente à la courbe (1ère)
CHOISIR
0 chapitre
592 . log
CHOISIR
0 chapitre
593 . Formule de Bessel
CHOISIR
0 chapitre
594 . la formule de Bessel
CHOISIR
0 chapitre
596 . Non classé
CHOISIR
0 chapitre
597 . Courbes paramétrées
CHOISIR
0 chapitre
598 . Formule de Parceval
CHOISIR
0 chapitre
599 . exp
CHOISIR
0 chapitre
600 . Fonctions circulaires-généralités
CHOISIR
0 chapitre
601 . La formule de Parceval
CHOISIR
0 chapitre
602 . Calcul de limites
CHOISIR
0 chapitre
604 . L'original
CHOISIR
0 chapitre
605 . Original dans les équa. diff et fonctions de transfert
CHOISIR
0 chapitre
606 . La division par une fraction
CHOISIR
0 chapitre
607 . signaux avancés
CHOISIR
0 chapitre
608 . les signaux avancés
CHOISIR
0 chapitre
609 . Loi uniforme
CHOISIR
0 chapitre
610 . Loi normale et proba
CHOISIR
0 chapitre
611 . la loi normale et proba
CHOISIR
0 chapitre
612 . racine carrée (term) : au dénominateur
CHOISIR
0 chapitre
613 . racine carrée (BTS) : au dénominateur
CHOISIR
0 chapitre
614 . Fractions : la division
CHOISIR
0 chapitre
615 . Racines n-ièmes de l'unité
CHOISIR
0 chapitre
616 . les racines n-ièmes de l'unité
CHOISIR
0 chapitre
617 . la TFD inverse
CHOISIR
0 chapitre
618 . TFD inverse
CHOISIR
0 chapitre
619 . Les puissances
CHOISIR
0 chapitre
621 . circulaires-généralités
CHOISIR
0 chapitre
622 . Droites et systèmes
CHOISIR
0 chapitre
623 . La loi normale centrée réduite
CHOISIR
0 chapitre
625 . Application de la formule : L(f(t -a) U(t - a)) = exp(-ap) F(p)
CHOISIR
0 chapitre
626 . Original pour les équa. diff et fonction de transfert
CHOISIR
0 chapitre
627 . Fractions : division par une fraction
CHOISIR
0 chapitre
628 . définition de la transformée en Z
CHOISIR
0 chapitre
629 . la déf. de la transformée en Z
CHOISIR
0 chapitre
630 . loi normale
CHOISIR
0 chapitre
631 . calcul de proba. entre le modèle discret et continue
CHOISIR
0 chapitre
632 . fonction sin
CHOISIR
0 chapitre
635 . Les racines carrées
CHOISIR
0 chapitre
636 . Fonction et composition
CHOISIR
0 chapitre
637 . Application de la formule L(f(t -a) U(t - a)) = exp(-ap) F(p)
CHOISIR
0 chapitre
638 . théorème du retard
CHOISIR
0 chapitre
639 . le théorème du retard
CHOISIR
0 chapitre
640 . Original avec la formule L(f(t -a) U(t - a)) = exp(-ap) F(p)
CHOISIR
0 chapitre
641 . loi normale et changement de variable
CHOISIR
0 chapitre
642 . loi normale et calcul de proba
CHOISIR
0 chapitre
643 . Approx. d'une loi binomiale par une loi normale
CHOISIR
0 chapitre
644 . sin
CHOISIR
0 chapitre
645 . fonction cos
CHOISIR
0 chapitre
648 . Application de la formule L(f(t) exp( -at) U(t)) = F(p + a)
CHOISIR
0 chapitre
649 . théorème de l'avance
CHOISIR
0 chapitre
650 . le théorème de l'avance
CHOISIR
0 chapitre
651 . L'original avec la formule L(f(t -a) U(t - a)) = exp(-ap) F(p)
CHOISIR
0 chapitre
652 . calcul de proba entre le discret et continu
CHOISIR
0 chapitre
653 . le calcul de proba dans les cas discret ou continu
CHOISIR
0 chapitre
654 . la somme de variables indépendantes
CHOISIR
0 chapitre
655 . cos
CHOISIR
0 chapitre
656 . fonction tan
CHOISIR
0 chapitre
658 . Fonction arctan
CHOISIR
0 chapitre
659 . Application de la formule : L(f(t) exp( -at) U(t)) = F(p + a)
CHOISIR
0 chapitre
660 . L'original avec la formule L(f(t) exp( -at) U(t)) = F(p + a)
CHOISIR
0 chapitre
661 . Recherche de l'original
CHOISIR
0 chapitre
662 . Original avec la TDZ
CHOISIR
0 chapitre
663 . Approximation d'une loi binomiale par une loi normale
CHOISIR
0 chapitre
664 . Approcher une loi binomiale par une loi normale
CHOISIR
0 chapitre
665 . tan
CHOISIR
0 chapitre
667 . Avec une primitive
CHOISIR
0 chapitre
668 . Arctan
CHOISIR
0 chapitre
669 . Original avec la formule L(f(t) exp( -at) U(t)) = F(p + a)
CHOISIR
0 chapitre
670 . Résoudre des équations de récurrence
CHOISIR
0 chapitre
671 . Résolution des équations de récurrence
CHOISIR
0 chapitre
672 . Somme de variables indépendantes
CHOISIR
0 chapitre
673 . somme de variables aléatoires indépendantes
CHOISIR
0 chapitre
675 . TDL avec une primitive
CHOISIR
0 chapitre
TOUTES LES VIDÉOS DU CHAPITRE
- ⭐️ Flashmaths ⭐️ : "bases sur les complexes" série 01
- synthèse sur les bases sur les complexes
- rituel 64 (et pas 63 !!) - calculer la dérivée de ces 4 fonctions
- rituel 63 - identification, polynômes et systèmes
- rituel 62 - calcul de 1er termes d'une suite récurrence et polynômes et identification
- point bilan sur les polynômes et l'identification
- rituel XLI - tfd et tfd inverse (transformée de Fourier Discrète)
- point bilan sur la Transformée de Fourier Discrète inverse (tfd)
- rituel 61- calcul de termes d'une suite définie par récurrence et transformation d'une équation de récurrence
- point bilan sur les suites récurrentes
- point bilan sur la formule Bessel chez la tfd (transformée de Fourier Discrète)
- rituel XL - calcul de la tfd (transformée de Fourier Discrète) avec les matrices
- pt bilan sur la tfd (transformée de fourier discrète) et la fft (fast fourier transform)
- rituel IXXXX - calcul de la tfd d'un signal
- point bilan sur les suites
- rituel 60 : calcul sur les suites
- [Tuto] : évolution de la rosace à 24 branches
- [Tuto] : apprendre à créer une rosace un peu plus grande
- [Tuto] : apprendre à créer la rosace
- J’ai ouvert grands les yeux dans mon jardin et j y ai vu la géométrie !! (partie 2)
- J’ai ouvert grands les yeux dans mon jardin et j y ai vu la géométrie !! (partie 1)
- [Tuto] : évolution de la rosace à 12 branches
- rituel 59 - résolution de 2 systèmes avec les matrices
- point bilan sur la résolution de système avec les matrices
- rituel 58 - trouver la matrice inverse
- synthèse sur la loi normale
- rituel IIXXXX - loi binomiale, de Poisson et loi Normale
- point bilan : l'inverse d'une matrice
- rituel 57 - matrices, multiplication et système
- rituel 56 - mise en lien des complexes avec la fonction de transfert et log
- point bilan : approximation de la loi binomiale par deux lois : Poisson et Normale
- rituel XXXVII - calcul de probabilité avec la loi normale
- synthèse sur les complexes
- ⭐️ Flashmaths ⭐️ : "bases sur les complexes" série 01
- rituel XXXVI - les lois discrètes et continues, et calcul de proba sur la loi normale
- point bilan - calcul de probabilités avec la loi normale et 3 valeurs à connaître
- Découvrir, à partir de la rosace, différentes structures pour vos coeur de mandalas ou mandalas...
- point bilan sur les complexes, fonction de transfert et la fonction log...
- rituel 55 - application des formules sur le module de complexes
- point bilan sur la loi normale
- rituel XXXV : rappel sur le calcul de probabilités pour des variables aléatoires continues
- comprendre le lien entre la loi uniforme et la loi normale grâce à Geogébra
- point bilan sur les propriétés sur le module et l'argument
- rituel 54 : lien entre forme algébrique et trigonométrique
- défi1 : créer un mandala à partir de motifs donnés
- Atelier pour apprendre à créer des kolams (grille de points alignés 4 par 4)
- Atelier pour apprendre pas à pas à dessiner un quart de mandala
- apprendre à dessiner un mandala zellige - étoile à 8 branches
- Atelier pour apprendre à créer des kolams (grille de points alignés 3 par 3)
- point bilan : lien entre la forme algébrique et la forme trigonométrique d'un complexe
- rituel 53 : calcul de modules et d'arguments
- Réalisation d'un mandala en noir et blanc, partagé en 32 parts
- démonstration de la création d'un mandala en accéléré.. Bientôt vous apprendrez à le faire ;-)
- Atelier pour apprendre à faire un mandala avec des éléments de la nature (à partir de 3 ans)
- Atelier pour apprendre à faire un mandala en fonction de vos envies pour votre goûter
- rituel XXXIV - transformée en Z et fonction de transfert
- rituel 52 - la forme trigonométrique (placer dans le plan et calcul)
- point bilan : la forme trigonométrique d'un complexe. comment la calculer ?
- point bilan - rappel sur la forme algébrique d'un complexe et découverte de la forme trigonométrique
- rituel XXXIII - original et transformée en Z + 1 exercice type
- rituel 51 - placer un complexe sous forme algébrique dans le plan et rappel sur les racines carrées
- Atelier pour apprendre à faire un mandala de fruits (pour des enfants à partir de 3 ans)
- A quoi va servir l'original chez la transformée en Z
- rituel 50 - interpréter les nombres dans un arbre de probabilités pondéré
- rituel 49 - tableau double entrée et probabilités conditionnelles
- rituel 48 - probabilités et proba. conditionnelles, interprétation
- point bilan transformée en Z et original d'un signal
- rituel XXXII - transformée en Z - rappel
- point bilan : synthèse 1 sur les lois discrètes et continues
- rituel 47 - probabilités et proba. conditionnelles
- rituel 46 - probabilités les bases...
- point bilan - probabilités conditionnelles et indépendance entre les événements
- point bilan -les probabilités conditionnelles
- rituel XXXI - probabilité et la loi exponentielle
- chercher l erreur puis corrigez-la avec la fonction exponentielle
- chercher l erreur puis corrigez-la avec la fonction log
- chercher l erreur puis corrigez-la avec la fonction ln (partie 2)
- chercher l erreur puis corrigez-la avec la fonction ln (partie 1)
- ds - CORRECTION - ln, log, exponentielle - partie 3
- ds - CORRECTION - ln, log, exponentielle - partie2
- ds - CORRECTION - ln, log, exponentielle - partie1
- rituel XXX - loi binomiale, approximation par une loi de Poisson, calcul de proba
- point bilan : la loi exponentielle
- point bilan : la loi uniforme
- point bilan : Loi de probabilité - Passage du discret au continu
- rituel 44 - log, ln et exp
- rituel 45 - ln, exp
- rituel IXXX - loi de poisson
- point bilan : approximation d'une loi binomiale par une loi de Poisson
- point bilan : calcul de probabilités avec la loi de Poisson
- point bilan sur intégrale et aire
- point bilan sur la fonction exponentielle
- Point bilan sur la fonction ln et la fonction log
- rituel 43 - ln
- loi de Poisson (avec rappel sur la loi binomiale)
- Créer ce mandala sur une base de 18
- dessiner une pièce d 'un puzzle ou un puzzle
- Structure de base d'un mandala sur une rythmique en 18
- toutes valeurs sur le cercle trigonométrique de 0 jusqu à 2pi
- mémento : forme trigonométrique d'un complexe
- mémento : forme trigonométrique : Ex2 : donner la forme trigo à partir de l'algébrique
- mémento : forme trigonométrique : ex1 à partir d'une forme trigo donnée
- complexes : i en maths, j en physique
- Formule 4 : exp(a) / exp(b) = exp(a - b)
- ex 5 : transformer l'expression exp(-n*pi/3)^2/exp(n*pi/2)^3 sous une forme exp(A)
- ex 4 : transformer l'expression exp(n*pi/2)^4 sous une forme exp(A)
- ex 2 : transformer l'expression exp(x - 2)^2 sous une forme exp(A)
- ex 1 : transformer l'expression exp(x + 3)*exp(2x + 1) sous une forme exp(A)
- ex 3 : transformer l'expression exp(2)*exp(3)*(1/exp(4))*(exp(-2))^(-3) sous une forme exp(A)
- formule 3 : 1/(exp(a)) = exp( - a)
- formule 2 : (exp(a))^b = exp(a * b)
- formule 1 : exp(a+b) = exp(a) * exp(b)
- Généralisation : trouver la matrice de la TFD inverse à partir de celle de la TFD
- la fft : Pour n = 3 avec Xcas : c) la démarche
- la fft : Pour n = 3 avec Xcas : b) donner la matrice de la fft sous forme algébrique
- La fft : Pour n = 3 avec Xcas : a) introduction
- Comparaison entre les formules de la TFD et TFD inverse
- TFD inverse pour n = 3 : 5/ trouver la matrice A
- TFD inverse pour n = 3 : 4/ conclusion sur la forme de (x0, x1, x2)
- TFD inverse pour n = 3 : 3/ trouver x2
- TFD inverse pour n = 3 : 2/ trouver x1
- TFD inverse pour n = 3 : 1/ trouver x0
- La TFD inverse, sa formule
- La formule de Bessel
- Ex : 2/ vérifier l'application de la formule de Bessel
- Ex : 1/ donner la TFD de (1,0,2,0)
- TFD sur une séquence avec 3 éléments : 4/ conclusion
- calculer la transformée de Fourier Discrète de la séquence (0,1,0)
- TFD sur une séquence avec 3 éléments : 2/ calcul de X2
- TFD sur une séquence avec 3 éléments : 2/ calcul de X1
- TFD sur une séquence avec 3 éléments : 1/ calcul de X0
- TFD sur une séquence avec 2 éléments : 3/ conclusion
- TFD sur une séquence avec 2 éléments : 2/ calcul de X1
- TFD sur une séquence avec 2 éléments : 1/ calcul de X0
- Définition de la transformée de Fourier discrète (TFD)
- Définition d'une loi exponentielle
- Avec la loi exponentielle, calculer P(X supérieur à d)
- Avec la loi exponentielle, calculer P(X inf. à c) : 3/ exprimer P(X inf à c) en fonction de lambda
- Avec la loi exponentielle, calculer P(X inf. à c) : 1 et 2/ exprimer cette proba et hachurer sur le dessin
- Avec la loi exponentielle, 2 et 3/calculer P(X compris entre c et d) et hachurer cette partie
- Avec la loi exponentielle, calculer P(X compris entre c et d) : 1/ que vaut f(x), la loi de densité
- Théorème d'approximation d'une loi binomiale par une loi de Poisson
- définition de la loi de Poisson
- 2/ quelle est la proba que le lot ait au plus 1 bouteille défectueuse?
- 1/ quelle est la proba que le lot ait 2 bouteilles défectueuses?
- 3/quelle est la probabilité que le standard reçoive au moins 8 appels?
- 2/quelle est la probabilité que le standard reçoive moins de 8 appels?
- 1/ quelle est la probabilité que le standard reçoive exactement 11 appels?
- Interprétation de la limite en - infini de la fonction exponentielle
- Synthèse sur la fonction exponentielle
- Définition du log (logarithme décimal)
- Exemple avec log décimal : 2/ Calculer GdB(w0) et donner une valeur approchée
- Exemple avec log décimal : 1/ montrer que GdB (w) = ....
- Synthèse pour la fonction cosinus
- Tracer de la courbe de cosinus : 3/ synthèse et tracer
- Tracer de la courbe de cosinus : 2/ tableau de valeurs
- Tracer de la courbe de cosinus : 1/ rappel des diverses propriétés graphiques
- Théorème sur la somme de n racines n-ième successives de l'unité
- soit z^6=1 et w = exp(i*pi/3). 4. calculer la somme pour k = 0 à 5 des w^k
- soit z^6=1 et w = exp(i*pi/3). 2/ donner la forme algébrique des 6 racines et les placer
- soit z^6=1 et w = exp(i*pi/3). 1/ donner les 6 racines 6-ième de l'unité
- Application : calculer la somme des 4 racines 4-ième de l'unité successive
- Toutes les mesures principales sur le cercle trigonométrique
- on a H(p) = 1/((p+2)(p+1)). 2/ Mq : H(jw) = (1/w) . (1/((2/w-w)+3j) (partie2)
- on a H(p) = 1/((p+2)(p+1)). 2/ Mq : H(jw) = (1/w) . (1/((2/w-w)+3j) (partie 1)
- on a H(p) = 1/((p+2)(p+1)). 1/que vaut H(jw)?
- Théorème les racines n-ièmes de l'unité sont ....
- z^4 = 1 : nombre de solutions et valeurs des racines + interprétation graphique
- z^3 = 1 : nombre de solutions et valeurs des racines + interprétation graphique
- z^2 = 1 : nombre de solutions et valeurs des racines + interprétation graphique
- Généralisation : comprendre la forme générale des solutions de z^n = 1
- Définition : les racines n-ièmes de l'unité
- Pour n = 3. Comprendre comment résoudre z^3 = 1 ? (partie 2)
- Pour n = 3. Comprendre comment résoudre z^3 = 1 ? (partie 1)
- Forme exponentielle du quotient de 2 complexes
- Connaissant z1 et z2 : placer les points d affixe respectives z1, z2 et z1 / z2
- Connaissant z1 et z2, donner la forme exponentielle de z1/z2
- Forme exponentielle de l'inverse d'un complexe
- z = 2 exp( - i *pi/3) : 2/ Placer M d'affixe z et M' d'affixe 1/z
- z = 2 exp( - i *pi/3) : 1/ donner la forme exponentielle de 1/z
- Forme exponentielle de la puissance d'un complexe
- w = exp(i*pi/4) : 2/ donner la forme algébrique de w^(-p) pour p compris entre 0 et 7
- w = exp(i*pi/4) : 1/ sur le cercle trigo, placer w^k pour k compris entre - 8 et 8 (partie2)
- w = exp(i*pi/4) : 1/ sur le cercle trigo, placer w^k pour k compris entre - 8 et 8 (partie1)
- z = 2 exp(- i * pi/4) : 2/ Placer M d'affixe z et M' d'affixe z^2
- z = 2 exp(- i * pi/4) : 1/ donner la forme exponentielle de z^2
- Forme exponentielle du produit de 2 complexes
- Exo sur cos et sin de pi/12 : 5/ en déduire les valeurs exactes de cos(pi/12) et sin(pi/12)
- Exo sur cos et sin de pi/12 : 4/ en déduire la forme algébrique de z3 (partie 2)
- Exo sur cos et sin de pi/12 : 4/ en déduire la forme algébrique de z3 (partie 1)
- Exo sur cos et sin de pi/12 : 3/Montrer que z1 x z2 = 2 z3 avec z3 = exp(i*pi/12)
- Exo sur cos et sin de pi/12 : 2/donner la forme algébrique de z2 = exp(- i *pi/4)
- Exo sur cos et sin de pi/12 : 1/ donner l'écriture algébrique de z1 = 1+irac(3)
- Connaissant z1 et z2 : placer les points d affixe respectives z1, z2 et z1 x z2
- Connaissant z1 et z2, donner la forme exponentielle de z1 x z2
- Forme exponentielle du conjugué d'un complexe
- z = 3 exp(-i*pi/6) : placer M d'affixe z et M' d'affixe le conjugué de z
- z = 3 exp(-i*pi/6) : donner la forme exponentielle du conjugué de z
- Définition : la forme exponentielle d'un nombre complexe
- z = - 1 : donner la forme trigonométrique et exponentielle de z
- z = - 2 rac(3) - 2i : donner la forme trigonométrique et exponentielle de z
- z = 1 - i : donner la forme trigonométrique et exponentielle de z
- z' = - 2exp(i*pi/2) : donner la forme algébrique
- z' = - 2exp(i*pi/2) : donner le module et un argument
- z = 3exp(i*pi/6) : donner la forme algébrique de z
- z = 3exp(i*pi/6) : donner le module et un argument
- Placer les 4 points d'affixe : z=exp(i*3*pi/4) ; z=exp(-i*pi/3) ; z = 2exp(- i*5pi/6) et z = 3 exp(i*pi/2)
- Définition d'un nouveau complexe : exponentielle i théta
- Valeur particulière à connaître : que vaut exp(- i *pi/2) ?
- Valeur particulière à connaître : que vaut exp(i *pi/2) ?
- Valeur particulière à connaître : que vaut exp(i *0) ?
- Valeur particulière à connaître : que vaut exp(i *pi) ?
- Principe pour résoudre un système d'équations grâce aux matrices (partie 2)
- Application sur la résolution d'un système avec les matrices
- EX2 : résoudre ce système avec les matrices si c est possible
- EX1 : résoudre ce système avec les matrices si c est possible
- Principe pour résoudre un système d'équations grâce aux matrices (partie 1)
- On donne un système d'équations linéaires, on veut le transformer sous forme matricielle
- On donne la matrice A et 2 vecteurs colonnes X et B, donner AX puis en déduire AX = B
- Définition : la matrice A est inversible
- Avec la calculatrice, trouver, lorsque c'est possible, l'inverse de 2 matrices
- Avec la calculatrice, montrer que A et B sont inverses l'une de l'autre
- Cette matrice est-elle inversible? si oui que vaut son inverse? (partie 2)
- Cette matrice est-elle inversible? si oui que vaut son inverse? (partie 1)
- Comprendre pourquoi chercher à inverser une matrice
- Calculer A x B et B x A. Que pouvez-vous en conclure?
- Si A et B sont indépendants, que vaut P(AIB) ?
- B "tirer un coeur" C ="tirer un as rouge". B et C sont ils indépendants?
- A ="tirer un as" B "tirer un coeur". A et B sont ils indépendants?
- Ex. avec les défauts e et l : 3/ probabilité d'avoir aucun défaut
- Ex. avec les défauts e et l : 2/ probabilité d'avoir au moins 1 défaut
- Ex. avec les défauts e et l : 1/ probabilité d'avoir les 2 défauts
- Définition : événements indépendants
- Définition des probabilités conditionnelles
- Proba dans une classe : 3.c/ et 4/ Calculer P(A inter B)/P(A) puis comparer avec fA(B)
- Proba dans une classe : 3.b/ Qui est A inter B ? que vaut P(A inter B) ?
- Proba dans une classe : 3.a/ Calculer P(A)
- Proba dans une classe : 2/b. Calculer la fréquence de B sachant A
- Proba dans une classe : 2/A) calculer la fréquence de B
- Proba dans une classe : 1/ Compléter le tableau
- Interprétation graphique de la tangente à la courbe en un point
- f(x) = (ax+b)exp(-2x) : 4/ Equation de la tangente en 0
- f(x) = (ax+b)exp(-2x) : 3/ Variations de f - (b) signe de f '(x) et conclusion
- f(x) = (ax+b)exp(-2x) : 3/ Variations de f - (a) résoudre f '(x) = 0
- f(x) = (ax+b)exp(-2x) : 2/ trouver a et b tel que f(0) = 1 et f '(0) = 3
- f(x) = (ax+b)exp(-2x) : 1/ calculer f '(x)
- g(x) = 3x^2-4x-1 : 2/ tracer de la tangente T à la courbe au point d abscisse 1
- g(x) = 3x^2-4x-1 : 1/équation de la tangente en 1 : c) simplification pour obtenir l'éq
- g(x) = 3x^2-4x-1 : 1/équation de la tangente en 1 : (b) calcul de g(1) et g'(1)
- g(x) = 3x^2-4x-1 : 1/équation de la tangente en 1 : (a) traduction de l'énoncé
- f(x) = x(x - 3) : 2/ tracer l'équation de la tangente au point d'abscisse 2
- f(x) = x(x - 3) : 1/ que vaut f'(2)?
- Equation de la tangente à la courbe au point A d'abscisse a
- Point méthode pour dresser le tableau de variation d'une fonction
- f(t) = t^3/3-t^2/2-6t+2 : 3/ Déterminer alors les variations de f
- f(t) = t^3/3-t^2/2-6t+2 : 2/ En déduire le signe de f'(t) (partie 2)
- f(t) = t^3/3-t^2/2-6t+2 : 2/ En déduire le signe de f'(t) (partie 1)
- f(t) = t^3/3-t^2/2-6t+2 : 1/ Calculer f'(t)
- Sens de variation de f, signe de la dérivée f'
- On nous donne H(jw). Que vaut une argument phi(w) de H(jw) ?
- On nous donne H(jw). Que vaut le module r(w) de H(jw) ? (partie 2)
- On nous donne H(jw). Que vaut le module r(w) de H(jw) ? (partie 1)
- On nous donne H(p). Comment obtenir H(jw) avec j le complexe tel que j^2 = - 1
- Formule 5 : ln(rac(a)) = 1/2 * ln(a)
- déterminer D tel que : ln(D)= 2 ln(x+3)+ ln(2x+1)
- transformer ln(x^2 rac(1+x^2))
- transformer ln(1/rac(x)
- Exprimer en fonction de ln(2) la quantité : ln (64e)
- Exprimer en fonction de ln(2) la quantité : ln (e/32)
- Exprimer en fonction de ln(2) la quantité : ln (2/e)
- Exprimer en fonction de ln(2) la quantité : ln (racine de 32)
- Exprimer en fonction de ln(2) la quantité : ln (2 e^2)
- Exprimer en fonction de ln(2) la quantité : ln(8)
- Exprimer B = 1/2 * ln(9) - 2 ln(3) à l'aide d'un seul ln
- Exprimer A = 2ln(3) + ln(2)+ln(1/2) à l'aide d'un seul ln
- Exprimer ln(8/9) en fonction de ln(2) et ln(3)
- Exprimer ln(24) en fonction de ln(2) et ln(3)
- Exprimer en fonction de ln(2) la quantité : ln(1/2)
- simplifier ln(rac(e))
- simplifier ln(6) - ln(2)
- Formule 4 : ln(1/a) = - ln(a)
- formule 3 : ln(a/b) = ln(a) - ln(b)
- Interprétation graphique de la limite de ln en 0
- Synthèse pour la fonction logarithme népérien (ln)
- Synthèse pour la fonction sinus
- Astuce pour retenir les Dérivées de sin et cos
- Tracer de la courbe de sinus : 3/ synthèse et tracer
- Tracer de la courbe de sinus : 2/ tableau de valeurs
- Tracer de la courbe de sinus : 1/ rappel des diverses propriétés graphiques
- Interprétation graphiques des limites de Arctan
- formule 2 : ln(a^m) = m * ln(a)
- Simplifier ln(16)
- formule 1 : ln(a*b) = ln(a) + ln(b)
- Interprétation graphique des limites de la fonction f(x) = 1/x
- Synthèse pour la fonction inverse
- Astuce pour ôter une racine d'un nombre au dénominateur
- Simplifier d = - 10/(3 rac(50))
- Simplifier c = 4/rac(28)
- Simplifier b = rac(6)/rac(27)
- Simplifier a = 3/rac(2)
- Racine carrée : DANGER 3
- Simplifier Q = 2 rac(5) - 3 rac(5) + rac(80)
- Simplifier P= rac(5) + 4 rac(5)
- Simplifier O = rac((3 - 7)^2)
- Simplifier N = rac(5^2 + 4)
- Simplifier M = rac(2^2 + 3^2)
- Racine carrée : DANGER 2
- Racine carrée : DANGER 1
- Formule 2 : racine carrée d'un quotient
- Simplifier L = rac(3) * rac(25/3)
- Simplifier K = 2 /rac(7) * rac(14)/rac(2)
- Simplifier J = 1 /rac(5) * rac(45)/7
- Simplifier I =rac(27)* rac(2)/rac(9)
- Formule 1 : racine carrée d'un produit
- Simplifier E = rac(2^2 * 3^2)
- simplifier H = 3 rac(8) * rac(18)
- Simplifier G = rac((7) *rac( 28)
- Simplifier F = rac(81 * 7^2)
- Simplifier D = (2 rac(3))^2
- Simplifier : C = rac(48)
- Simplifier : B = rac(24)
- Simplifier : A = rac(18)
- Synthèse pour la fonction racine carrée
- Synthèse pour la fonction carrée
- Synthèse pour les fonctions affines (partie 2)
- Synthèse pour les fonctions affines (partie 1)
- Définition d'une fonction affine, linéaire, constante
- Repère et nombres complexes
- Identifier des complexes dans le plan
- Comment obtenir la courbe de f(x+A) à partir de celle de f(x), avec A réel ?
- Identification et fct rationnelle : 4/ Identifier avec les polynômes des numérateurs
- Recherche de réels avec des fractions : a) réduction au même dénominateur
- Recherche de réels avec des fractions : b) identification
- Recherche de réels avec des fractions : c) résolution du système
- Identification et fct rationnelle : 3/ Vérifier les dénominateurs
- Identification et fct rationnelle : 2/ Regrouper les éléments de la même famille
- Identification et fct rationnelle : 1/ réduire au même dénominateur
- Définition d'une fonction rationnelle
- Remarque : pourquoi une telle la différence entre b et e?
- Reconnaître les fonctions rationnelles dans d et e.
- Reconnaître les fonctions rationnelles dans a. b. et c.
- Démarche pour donner les valeurs du cos et sin d un angle quelconque
- Valeur du cos et sin de 2pi/3
- Valeur du cos et sin de - pi/4
- Valeur du cos et sin de 3pi/2
- Valeur du cos et sin de - 5pi/6
- Comprendre les séries en marchant sur une droite graduée
- Rappel des propriétés d'une fonction impaire (courbe, déf. intégrale sur un intervalle centré)
- Prop. de l'intégrale pour une fct périodique : a) définition de la périodicité
- Prop. de l'intégrale pour une fct périodique : b) la propriété
- Prop. de l'intégrale pour une fct périodique : c) pour un intervalle centré
- Ex : b) calcul de l'intégrale de f sur [- pi ; pi]
- Ex : a) tracer de la courbe
- Application : c) calcul de l'intégrale de f(t) cos(nwt) sur 0 ; pi] (3) calcul
- Application : c) calcul de l'intégrale de f(t) cos(nwt) sur 0 ; pi] (2) Schéma d'intégration
- Application : c) calcul de l'intégrale de f(t) cos(nwt) sur 0 ; pi] (1) réduction
- Application : b) calcul de l'intégrale de f sur [0 ; pi]
- Application : a) tracer de la courbe représentative de f
- Ex : c)pour n entier naturel non nul, calcul de l'intégrale de f(t)cos(nwt) sur [- pi ; pi]
- Ex : d)calcul de l'intégrale de f(t)sin(nwt) sur [- π ; π] (2) calcul
- Ex : d)calcul de l'intégrale de f(t)sin(nwt) sur [- pi ; pi] (1) réduction
- Intégrale sur [-pi ; pi] de f(t)sin(nt) avec f impaire et 2-pi périodique : b)valeur suivant n
- Intégrale sur [-pi ; pi] de f(t)sin(nt) avec f impaire et 2-pi périodique : a)calcul
- Intégrale sur [-pi ; pi] de f(t)cos(nt) avec f impaire et 2-pi périodique
- introduction sur les séries de Fourier
- Vocabulaire sur les séries de Fourier et les coefficients de Fourier
- Interprétation graphique du développement en série de Fourier d'une fonction périodique donnée
- Les formules pour calculer les coefficients de Fourier
- Avec une fonction constante par morceaux : 4/ Calcul de b(n)
- Avec une fonction constante par morceaux : 3/ Calcul de a(n)
- Avec une fonction constante par morceaux : 2/ Vérification avec la valeur moyenne
- Avec une fonction constante par morceaux : 2/ Calcul de a(0)
- Avec une fonction constante par morceaux : 1/ Tracer la courbe
- Avec une fonction constante par morceaux : 5/Développement en série de Fourier
- Ex. avec f(t) = t sur [0 ; π[ une fonction π-périodique : 1/ Tracer de la courbe
- Ex. avec f(t) = t sur [0 ; π[ : 3/ développement en série de Fourier
- Ex. avec f(t) = t sur [0 ; π[ : 2/ Calcul de b(n) - calculs finaux
- Ex. avec f(t) = t sur [0 ; π[ : 2/ Calcul de b(n) - Intégration par partie
- Ex. avec f(t) = t sur [0 ; π[ : 2/ Calcul de b(n) - transformation de l'intégrale
- Ex. avec f(t) = t sur [0 ; π[ : 2/ calcul de a(n) - Calculs finaux
- Ex. avec f(t) = t sur [0 ; π[ : 2/ calcul de a(n) - Intégration par partie
- Ex. avec f(t) = t sur [0 ; π[ : 2/ calcul de a(n) - transformation de l'intégrale
- Ex. avec f(t) = t sur [0 ; π[ une fonction π-périodique : 2/ calcul de a(0)
- f PAIRE : simplification de a(0)
- f PAIRE : simplification de a(n)
- f PAIRE : simplification de b(n)
- f PAIRE : simplification de son développement en série de Fourier
- f IMPAIRE : simplification de a(0)
- f IMPAIRE : simplification de a(n)
- f IMPAIRE : simplification de b(n)
- Rappel des propriétés d'une fonction paire (courbe, définition, intégrale sur un intervalle centré)
- somme d'une suite géométrique : b) découverte de la formule
- Calcul de la somme : 3^0 + 3^1 + ...+ 3^10
- Notation pour les séries : a) découverte du symbole sigma sur un exemple
- Notation pour les séries : b) utilisation du symbole sigma avec les sommes partielles
- Ex : transformer en somme X1
- transformer en somme : sigma pour k = 0 à 5 de w^k avec w = exp(i*pi/3) (partie2)
- transformer en somme : sigma pour k = 0 à 5 de w^k avec w = exp(i*pi/3) (partie1)
- Détailler l'expression P avec des signes +
- Détailler avec des signes + la somme de j = 0 à 4 de 4j + 1
- Utiliser le symbole somme représenter pour : 1/3 + 1/4 + ... + 1/n
- Utiliser le symbole somme représenter pour : 1^2 + 2^2 + ... 26^2
- Le vocabulaire pour les séries, série convergente et divergente
- Justification de la marche sur une droite graduée
- Ex avec la somme partielle d'une suite arithmétique : b)que peut-on en déduire pour la série ?
- Ex avec la somme partielle d'une suite arithmétique : a) limite de S(n)
- Ex avec une suite géométrique : c) calculer la limite de S(n) la somme partielle
- Ex avec une suite géométrique : b) calculer la limite de u(n)
- Ex avec une suite géométrique : a) exprimer u(n) en fonction de n
- Série arithmétique : définition
- Etude de la convergence de la série arithmétique : 1+2+3+4+....
- Définition d'une série géométrique
- Critère de convergence pour les séries géométriques
- Etudier la convergence de la série des 2 (-1/3)^n
- Etudier la convergence de la série des 3^n
- définition des séries de Riemann
- Théorème de convergence pour les séries de Riemann
- Dire si les deux séries données sont convergentes ou non
- Définition des séries à termes positifs
- Définition de l'équivalence entre 2 suites et théorème d'équivalence pour un polynôme
- Trouver un équivalent de (2n - 1)^(-2)
- Trouver un équivalent de (3n^2 - 2n + 5)/(4n - 3)
- Trouver un équivalent de 3n^4 -5n + 3
- Critère de convergence pour les séries à termes positifs
- Etudier la convergence de la séries des rac(n)/(n - 1)
- Etudier la convergence de la séries des 3/(n^2 + 1)
- Suite arithmétique et le symbole sigma pour représenter une somme
- développer une expression avec le symbole sigma en une somme d'éléments
- Formule pour calculer la somme : 1+2+3+...+ n
- Application de la formule : 1+2+3+...+n = n(n+1)/2
- somme d'une suite géométrique : a) écriture avec le symbole sigma
- f IMPAIRE : simplification du développement en série de Fourier
- f impaire et f(t) = t sur ] -π; π[ : g) interprétation graphique du développement de Fourier
- f impaire et f(t) = t sur ] -π; π[ : f) développement en série de Fourier
- f impaire et f(t) = t sur ] -π; π[ : d) calcul b(n) 3- calculs finaux
- f impaire et f(t) = t sur ] -π; π[ : d) calcul b(n) 1- réduction de l'intégrale
- f impaire et f(t) = t sur ] -π; π[ : d) calcul b(n) 2- intégration par partie
- f impaire et f(t) = t sur ] -π; π[ : c) calcul a(n)
- f impaire et f(t) = t sur ] -π; π[ : b) calcul a(0)
- f impaire et f(t) = t sur ] -π; π[ : a) tracer de la courbe de f
- Tableau de rappel sur la parité et la primitive de cos ou sin
- La primitive de g(t) = 5 cos(3t)
- La primitive de f(t) = 4sin(t)
- Réduction des coefficients de Fourier si la fonction est paire ou impaire
- Pédagogie inversée : version basique... Une manière de faire...
- Pédagogie inversée : version avancée... Une autre manière de procéder...
- Comprendre une différence importante : a) tracer f(t - a) à partir de f donnée
- Comprendre une différence importante : b) tracer f(t - a)U(t) à partir de f donnée
- Comprendre une différence importante : c) tracer f(t - a)U(t-a) à partir de f donnée
- h(t) = 3 cos(t)U(t) : c) quelle est la valeur de h(t - pi/2) si t supérieur à pi/2 ?
- h(t) = 3 cos(t)U(t) : b) quelle est la valeur de h(t - pi/2) si t inférieur à pi/2 ?
- h(t) = 3 cos(t)U(t) : a) quelle est l'expression de h(t - pi/2) ?
- Principe de composition : a) recherche d'une image
- Principe de composition : b) expression de f(2t)
- Principe de composition : c) expression de f(t - 1)
- Principe de composition : d) sur une fonction causale g(t), donner g(t - 2)
- On pose g(t) = f(t - tau) U(t - tau). Trouver f et tau avec : d) j(t) = U(t -1)
- On pose g(t) = f(t - tau) U(t - tau). Trouver f et tau avec : c)g(t) = 5(t-3)^2U(t-3)
- On pose g(t) = f(t - tau) U(t - tau). Trouver f et tau avec : b)g(t) = sin(t -pi)U(t - pi)
- On pose g(t) = f(t - tau) U(t - tau). Trouver f et tau avec : a)g(t) = 2(t - 3) U(t - 3)
- Ex2 : comprendre la forme f(t -a) avec f donnée (principe de composition)
- Ex1 : comprendre la forme f(t -a) avec f donnée (principe de composition)
- 3 exemples sur l'expression de f(t - tau) avec f donnée
- Comment obtient-on la première identité remarquable?
- Développer (5x + 4)²
- développer : (2x + 1)^2
- Démonstration de la 2nde identité remarquable (1ière manière)
- Démonstration de la 2nde identité remarquable (2nd manière)
- Développer (3 - 2x)²
- développer (2 - 3x)²
- Démonstration de la 3ième identité remarquable
- Factoriser : 25 - 9(x -3)²
- Développer : 25 - 9(x -3)²
- factoriser (4x)² - 9
- définition de l'original
- Propriété de l'original et unicité
- Application : quel est l'original de F(p) = 1/p^2 ?
- a) quelle fonction a pour TDL : F(p) = 1/p ?
- c) quelle fonction a pour TDL : H(p) = 1/(p + 4) ?
- Recherche de l'original de F(p) = 1/(p(p +1)) : 3/ déterminer l'original f(t)
- Recherche de l'original de F(p) = 1/(p(p +1)) : 2/ recherche des originaux de : 1/p et 1/(p + 1)
- Recherche de l'original de F(p) = 1/(p(p +1)) : 1/ trouver a et b tq 1/(p(p + 1)) = a/p + b/(p + 1)
- Déterminer l'original de H(p) = 6/(p^2 + 4)
- Déterminer l'original de F(p) = - 3/(p + 2)
- Déterminer l'original de S(p) = - 4^/(p^2 + 9)
- Déterminer l'original de G(p) = 1/(3p)
- Déterminer l'original de F(p) = 1/p^3
- d) quelle fonction a pour TDL : S(p) = 4/(p^2 + 16) ?
- b) quelle fonction a pour TDL : G(p) = p/(p^2 + 4) ?
- Présentation générale de la pédagogie inversée
- Pourquoi ? comment faire des vidéos? Pour qui ?
- Différence entre la notion de fonction continue ou discontinue
- Exemple : trouver les valeurs de f(0+) et f(0-)
- réduire au même dénominateur : 1/p - 1/(p +20)
- définition intégrale généralisée
- étudier la convergence de l'intégrale de 1 à + infini de 1/t^2
- étudier la convergence de l'intégrale de 1 à + infini de 1/t
- Introduction sur la transformée de Laplace
- définition de la transformée de Laplace
- Comprendre l'utilisation de la Transformée de Laplace sur les équations différentielles
- Calcul de la transformée de Laplace de la fonction échelon unité
- Définition d'une fonction causale
- Ex avec f(t) = t : 3/ Exprimer la fonction causale en fonction de l'échelon unité
- Ex avec f(t) = t : 2/ Tracer la fonction causale associée
- Ex avec f(t) = t : 1/ tracer la courbe de f
- Application : rendre causale une fonction : 3/ exprimer en fonction de l'échelon unité
- Application : rendre causale une fonction : 2/tracer la fonction causale associée
- Application : rendre causale une fonction : 1/f est-elle causale?
- Fonction causale retardée
- Tableau des transformées de Laplace des fonctions usuelles
- donner la transformée de Laplace de : e) g(t) = cos(4t) U(t)
- donner la transformée de Laplace de : d) h(t) = sin(3t) U(t)
- donner la transformée de Laplace de : c) g(t) = exp(5t) U(t)
- donner la transformée de Laplace de : b) g(t) = exp(- 4t) U(t)
- donner la transformée de Laplace de a) f(t) = t^3 U(t)
- Propriété de linéarité de la transformée de Laplace : a) énoncé
- Propriétés de linéarité de la Transformée de Laplace : b) démonstration
- Donner la TDL de f(t) = (t^2 + 3t - 4)U(t) : 2/ réduction au même dénominateur
- Donner la TDL de f(t) = (t^2 + 3t - 4)U(t) : 1/application des formules
- Quelle est la transformée de Laplace de l'équation u(t) = R i(t) ?
- Quelle est la transformée de Laplace de l'équation i(t) = i1(t) + i2(t)
- Donner la TDL de f(t) = (2exp(-3t) + cos(t))U(t) : 1/application des formules
- Donner la TDL de f(t) = (2exp(-3t) + cos(t))U(t) : 2/ réduction au même dénominateur
- Application : Fonction de Transfert : 3/Transformée de Laplace de s(t)
- Application : Fonction de Transfert : 2/Transformée de Laplace de h(t)
- Application : Fonction de Transfert : 2/Transformée de Laplace de e(t)
- Application : Fonction de Transfert : 1/ tracer la courbe de e
- Donner la TDL de f(t) = (sin(3t)U(t) + 6 cos(3t)U(t))/3
- Explication des formules sur la TDL d'une dérivée première et seconde
- Lien entre la Transformée de Laplace de la dérivée première et la dérivée seconde
- Transformée de Laplace sur une équa. diff. du 2nd ordre : b) Expression de S(p)
- Transformée de Laplace sur une équa. diff. du 2nd ordre : a) transformation
- Donner la transformée de Laplace de l'équation : u(t) = L di/dt
- Mon parcours et comment l'idée des vidéos est venue...
- théorème de laplace sur une fonction retardée
- c) 1- donner la transformée de Laplace de U(t - 1)
- b/ donner la transformée de Laplace de f(t) = t U(t) - (t - 2)U(t - 2)
- a/ donner la transformée de Laplace de f(t) = 2(t - 3) U(t - 3)
- c) 2- en déduire la transformée de Laplace de f(t) = U(t - 1) - U(t - 2)
- d) donner la transformée de Laplace de e(t) = E(U(t) - U(t - tau)) avec E et tau des constantes
- Recherche de l'original de S(p) = (1 - exp(-ap))/p^2
- Recherche de l'original de G(p) = - exp(-3p)/p
- Recherche de l'original de F(p) = exp(-p)/(p^2 + 9) : 2/ déterminer alors l'original f(t)
- Recherche de l'original de F(p) = exp(-p)/(p^2 + 9) : 1/ trouver les valeurs de f et tau
- Recherche de l'original de G(p) = exp(-3p)/p^2
- Application : g) tracer l'allure de la courbe de s(t)
- Application : f) 2- Donner l'expression de s(t) pour t compris entre 0 et 1
- Application : f) 1- Donner l'expression de s(t) pour t inférieur à 0
- Application : e) Trouver l'original s(t) : 4- conclusion
- Application : e) Trouver l'original s(t) : 3- donner l'original de exp(-p)/(p+1)
- Application : e) Trouver l'original s(t) : 2- donner les originaux de 1/p ;1/(p+1) ; exp(-p)/p
- Application : e) Trouver l'original s(t) : 1-transformer l'expression de S(p)
- Application : d) Trouver a et b tel que :1/(p(p+1)) = a/p + b/(p+1)
- Application : c) Déterminer S(p) en fonction de p
- Application : b) Déterminer E(p)
- Application : a) déterminer l'expression de e(t) à partir de son graphe
- f impaire : b)calcul de l'intégrale de f(t)sin(nwt) sur [-a; a]
- Ex: 3. b) intégrale de f(t) sin (2nt) sur [- pi ; pi] avec le calcul formel
- Ex : 1. Tracer de la courbe
- Ex: 3. b) intégrale de f(t) sin (2nt) sur [- pi ; pi] (3) Calcul de l'intégrale
- Ex: 3. b) intégrale de f(t) sin (2nt) sur [- pi ; pi] (2) Schéma d'intégration
- Ex: 3. b) intégrale de f(t) sin (2nt) sur [- pi ; pi] (1) Réduction de l'intégration
- Ex: 3. a) intégrale de f(t) cos(2nt) sur [- pi ; pi]
- Ex : 2. f est-elle paire ? impaire? ou ni paire ni impaire?
- propriété : lien intégrale et aire pour une fonction positive
- Calcul de l'aire d'un domaine pour f(t) = 1/t sur [1;e]
- Calcul de l'aire d'un domaine pour la fonction échelon unité sur [0;5]
- Représentation graphique d'une suite : c) pourquoi une telle répartition des éléments ?
- Intro sur les suites récurrentes : a) calcul du capital sur le livret pour les 3 premières années
- Intro sur les suites récurrentes : b) comment estimer le capital au bout de 10 ans?
- définition d'une suite récurrente
- Exo complet sur une suite récurrente : d) sens de variation de la suite
- Exo complet sur une suite récurrente : c) représentation graphique de la suite
- Exo complet sur une suite récurrente : b) calcul de x(4) et x(5)
- Exo complet sur une suite récurrente : a) transformation de la relation de récurrence
- Suite v(n+1) = 5 v(n) - 2 : c) Calcul de v(3)
- Suite x(n) - 3 x(n-1) = 1 : d) valeur de x(3)
- Suite v(n+1) = 5 v(n) - 2 : a) Calcul de v(1)
- Suite v(n+1) = 5 v(n) - 2 : b) Calcul de v(2)
- Suite x(n) - 3 x(n-1) = 1 : b) valeur de x(1)
- Suite x(n) - 3 x(n-1) = 1 : a) valeur de x(0)
- Suite x(n) - 3 x(n-1) = 1 : c) valeur de x(2)
- Introduction sur les matrices en lien avec les tableaux
- Définition d'une matrice, de sa dimension et de ses coefficients
- donner une matrice de dimension 3x2 et une de dimension 2x2
- détails des coefficients pour une matrice de dimension nxp
- trouver la matrice correspondante...
- donner la dimension d'une matrice ainsi que des coefficients
- Matrice ligne et matrice colonne
- Matrice carrée
- Matrice diagonale
- Matrice unité
- Matrice nulle
- Egalité entre deux matrices
- La Somme de matrices
- Propriétés sur la somme de matrices
- Représentation graphique d'une suite : b) placer des points
- Représentation graphique d'une suite : a)calcul des 7 premiers termes
- 3. Interprétation graphique de l'intégrale pour une fonction NEGATIVE : a)calcul de l'aire
- 3. Interprétation graphique de l'intégrale pour une fonction NEGATIVE : b)expression de f
- 3. Interprétation graphique de l'intégrale pour une fonction NEGATIVE : c)calcul de l'intégrale
- 3. Interprétation graphique de l'intégrale pour une fonction NEGATIVE : d) synthèse
- propriété : lien intégrale et aire pour une fonction NEGATIVE
- Calcul de l'aire du domaine définie par f(x) = x^3/27-x²/3 sur [0;9]
- propriété : lien intégrale et aire pour une fonction de SIGNE QUELCONQUE
- Aire pour f(x) = x² - x - 2 sur [-1;3] : c) aire totale
- Aire pour f(x) = x² - x - 2 sur [-1;3] : b) aire lorsque f est négative
- Aire pour f(x) = x² - x - 2 sur [-1;3] : a) aire lorsque f est positive
- Relation de Chasles pour les intégrales
- Exo 2 sur la relation de Chasles
- Exo 1 sur Chasles : c) Interprétation graphique de l'intégrale
- Exo 1 sur Chasles : b) calcul de l'intégrale
- Exo 1 sur Chasles : a) Tracer de la courbe de f
- Intégrale et linéarité
- Application des propriétés de linéarité pour les intégrales
- Valeur moyenne de f sur un intervalle
- Valeur moyenne de f(t) = 1/t sur [1;e]
- Valeur moyenne de f sur une période
- application sur la valeur moyenne sur une période : b) calcul de la valeur moyenne
- application sur la valeur moyenne sur une période : a) tracer de la courbe de f
- Introduction sur les suites : a) explication avec les premiers termes
- Introduction sur les suites : b) retrouver le rang d'un élément de la suite
- Introduction sur les suites : c) généralisation
- Vocabulaire sur les suites
- Différence, pour les éléments d'une suite, entre IN et IN*
- Suite u(n)= 2n : a)calcul des 3 premiers termes
- Suite u(n) = 2n : b) calcul de u(20)
- Suite u(n) = 2n : c) Calcul de u(n + 1)
- Suite w(n) = 3^n : c) simplifier w(n + 1)/w(n)
- Suite w(n) = 3^n : b) calcul de w(n + 1)
- Suite w(n) = 3^n : a)calcul des 3 premiers termes
- Suite v(n) = n - 5 : d) simplifier v(n) - v(n - 1)
- Suite v(n) = n - 5 : c) calcul de v(n - 1)
- Suite v(n) = n - 5 : b) trouver n tel que v(n) = 67
- Suite v(n) = n - 5 : a) calcul des 3 premiers termes
- Suite u(n) = 2n : d) simplifier u(n+1) - u(n)
- Produit d'une matrice par un réel k
- Opposé d'une matrice
- propriétés sur le produit de matrices avec des réels
- Exemple avec le produit de matrices avec des réels
- expression en fonction de n
- Définition d'une suite géométrique (explication, exemple, généralisation)
- expression en fonction de n
- Composition et développement limité : la propriété
- dl4(0) de f(x) = exp(x) - exp(-x) : b) développement limité de la différence
- dl4(0) de f(x) = exp(x) - exp(-x) : a) dl4(0) de exp(-x)
- dl3(0) de f(x) = (x - 1)exp(2x) : b) développement limité du produit
- dl3(0) de f(x) = (x - 1)exp(2x) : a) dl3(0) de exp(2x)
- développement limité à l'ordre 7 en 0 de f(t) = sin(3t)
- Evolution de la trajectoire de M en fonction des variations de f et g
- Ex3 : b) A partir du tableau combiné, tracer l'allure de la courbe paramétrée
- Ex3 : a) tracer du tableau combiné des variations de f et g
- Vecteur tangent : définition
- vecteur tangent : cas particulier où l'une des coordonnées est nulle
- exemple : 1.b) tableau de signe de f '
- exemple : 1.a) calcul de la dérivée de f
- Exemple : 1.c) tableau de variation de f
- exemple : 2. calcul de la dérivée de g
- exemple : 5B. tracer l'allure de la courbe ainsi que la tangente en A
- exemple : 5A. tableau de valeurs de f et g
- exemple : 4. Vecteur tangent à la courbe au point de paramètre t = 0,5
- exemple : 3. tableau combiné de f et g
- valeur de cos(2 n pi) avec n appartenant à IN
- valeur de sin(2 n pi) avec n appartenant à IN
- valeur de cos( n pi) avec n appartenant à IN
- valeur de sin(n pi) avec n appartenant à IN
- Ex : calcul de l'intégrale de f(t) = 3cos(2t) entre 0 et pi/2
- Ex : calcul de l'intégrale de f(t) = sin(nt) entre 0 et pi, avec n appartenant à IN
- Ex : calcul de l'intégrale de f(x) = cos(nx) entre 0 et pi, avec n appartenant à IN
- Rappel des propriétés d'une fonction paire (courbe, définition, intégrale sur un intervalle centré)
- Rappel des propriétés d'une fonction impaire (courbe, déf. intégrale sur un intervalle centré)
- f paire : a)calcul de l'intégrale de f(t)cos(nwt) sur [-a; a]
- f paire : b)calcul de l'intégrale de f(t)sin(nwt) sur [-a; a]
- Calcul de l'intégrale sur [-1; 1] de f(t) sin(nt) avec f(t) = 2t sur [0;1]
- Calcul de l'intégrale sur [ -1 ; 1] de f(t) cos(nt) avec f(t) = 2t sur [0;1]
- Définition d'une suite arithmétique (explication, exemple, généralisation)
- Comment créer un tableau combiné des variations de f(t) et g(t) ?
- Parité et développements limités
- Développement limité d'un polynôme
- Exemples de dl pour des polynômes
- Dl et addition de fonctions
- Développement limité à l'ordre 3 en 0 de f(t) = exp(t) + 1/(1+t)
- Dl et produit de fonctions
- développement limité à l'ordre 2 en 0 de f(x) = exp(x)/(1 + x)
- Développement limité à l'ordre 3 en 0 de f(t) = sin(t) cos(t)
- Composition et développement limité : introduction
- Définition du produit d'un vecteur ligne par un vecteur colonne
- Exemple d'un produit d'un vecteur ligne par un vecteur colonne
- Produit de 2 matrices
- Explication du produit de matrices avec le détail des coefficients
- Disposition pratique pour faire le produit : a) vérification des dimensions
- Disposition pratique pour faire le produit : b) calcul du coefficient c11
- Disposition pratique pour faire le produit : c) calcul du coefficient c12
- Disposition pratique pour faire le produit : d) calcul du coefficient c13
- Disposition pratique pour faire le produit : e) calcul des coefficients de la 2° ligne
- Ex4 : puissances de matrices : b) calcul de D^3
- Ex4 : puissances de matrices : a) calcul de D^2
- Ex3 : calcul de CD : b) produit des 2 matrices
- Ex3 : calcul de CD : a) vérification de la dimension de CD
- Ex2 avec le produit de matrices : c-d) Calcul de BA
- Ex1 avec le produit de matrices : c) que dire de BA ?
- Ex1 avec le produit de matrices : a) calcul de la dimension de AB
- Ex2 avec le produit de matrices : a-b) Calcul de AB
- Ex1 avec le produit de matrices : b) calcul de AB
- Vocabulaire autour des courbes paramétrées
- Comment tracer une courbe paramétrée?
- Ex2 : b) tracer l'allure du système paramétrique
- Ex2 : a) dresser le tableau de valeurs de f(t) et g(t)
- Ex1: tracer de l'allure d'une courbe paramétrée à partir d'un tableau de valeurs
- f impaire : a)calcul de l'intégrale de f(t)cos(nwt) sur [-a; a]
- Application : quelle est la formule si on veut la transformée en Z de x(n - 1)?
- Solution d'équiprobabilité au modèle infini : a) introduction
- Solution d'équiprobabilité au modèle infini : b) questions
- Solution d'équiprobabilité au modèle infini : c) définition du calcul des proba.
- Solution d'équiprobabilité au modèle infini : d) généralisation sur un intervalle
- Définition de la loi uniforme
- Propriété : calcul d'une probabilité sur un sous intervalle avec la loi uniforme
- Espérance, écart-type et variance pour une loi uniforme
- Ex : 2/c) Calculer la probabilité que le facteur passe après 10h15
- Ex : 2/c) Calculer la probabilité que le facteur passe avant 10h20
- Ex : 2/b) Calculer la probabilité que le facteur passe entre 10h15 et 10h20
- Ex : 2/a) Calculer la probabilité que le facteur passe à 10h25 exactement
- Ex : 1/ quelle est la loi suit la variable aléatoire F?
- Ex : 3/ quelle est l'heure moyenne de son passage
- Synthèse sur la densité de proba. : tableau de variation, courbe, axe de sym., max
- Synthèse sur la densité de proba. de N : 2 probabilités facile à retenir
- La loi normale N(1;2)
- Propriété : Interprétation de P(X inférieur à a)
- Propriété : Interprétation de P(X supérieur à a)
- Propriété : Interprétation de P(X compris entre a et b)
- Ex avec N(100 ;0,43) et sa table : Donner P(X compris entre 99 et 101)
- Ex avec N(100 ;0,43) et sa table : Donner P(X supérieur à 99)
- Avec N(0;1) et sa table : Déterminer b tel que P(T supérieur à b) = 0,0853
- Avec N(0;1) et sa table : Déterminer a tel que P(T inférieur à a) = 0,7673
- Avec N(0;1) et sa table : Donner P(T supérieur à 1,95)
- Avec N(0;1) et sa table : en déduire P(T compris entre 0,2 et 1,67)
- Avec N(0;1) et sa table : donner P(T inférieur à 0,2)
- Avec N(0;1) et sa table : donner P(T inférieur à 1,67)
- 3 proba à connaître : 1/ mise en place du cadre
- 3 proba à connaître : 2/ Calculer P( X soit compris entre m - sigma et m + sigma)
- 3 proba à connaître : 3/ Calculer P( X soit compris entre m - 2sigma et m + 2sigma)
- Définition des probabilités pour une variable aléatoire continue
- Définition : lois de probabilités à densité
- Application : quelle est la formule si on veut la transformée en Z de x(n - 2)?
- trouver (Zx)(z) en appliquant la TEZ sur une équation de récurrence (partie1)
- quelle est la transformée en Z de s(n) = 4 e(n - 1)?
- quelle est la transformée en Z de s(n) = r(n - 2)?
- trouver (Zx)(z) en appliquant la TEZ sur une équation de récurrence (partie2)
- Théorème de l'avance pour un signal de type : x(n + 1)
- Théorème de l'avance pour un signal de type : x(n + 2)
- en appliquant la TEZ à 20y(n+1) - 21y(n)= e(n), trouver Y(z) (partie 1)
- Remarque : Pourquoi la transformée en Z de e(n+2) est la même que e(n)?
- quelle est la transformée en Z de s(n) = r(n + 1)?
- quelle est la transformée en Z de e(n + 2) ? (partie 2)
- quelle est la transformée en Z de e(n + 2) ? (partie 1)
- en appliquant la TEZ à 20y(n+1) - 21y(n)= e(n), trouver Y(z) (partie 2)
- Comment transformer l'intégrale de f^2 pour une fonction f est T-périodique
- c) f impaire : 3/ calcul du carré de la valeur efficace
- c) f impaire : 2/ calcul de la valeur moyenne
- c) f impaire : 1/ tracer la courbe de f
- b) f paire : 3/ calcul du carré de la valeur efficace
- b) f paire : 2/ calcul de la valeur moyenne
- b) f paire : 1/ tracer la courbe de f
- a) f quelconque : 3/ calcul du carré de la valeur efficace
- a) f quelconque : 2/ calcul de la valeur moyenne
- a) f quelconque : 1/ tracer la courbe de f
- Map sur la transformée en Z : définition et signaux de référence
- Map sur la transformée en Z : les propriétés
- Déterminer F(p + 2) sachant que F(p) = 3/p
- Déterminer G(p + 1) sachant que G(p) = 4/p^3
- Déterminer H(p + 3) sachant que H(p) = 2/(p + 5)
- Original de G(p) = 3!/(p-2)^4 : 1-trouver la TDL la plus proche de l'expression de G(p)
- Original de G(p) = 3!/(p-2)^4 : 2- Application de la formule et conclusion
- Donner l'original de G(p) = 1/(p+3)^2
- En électronique : 1/aux bornes de la résistance, exprimer U(p) en fonction de I(p)
- En électronique : 2/aux bornes de la bobine, exprimer U(p) en fonction de I(p)
- En électronique : 3/aux bornes du condensateur, exprimer U(p) en fonction de I(p)
- En électronique : 4/ L'impédance de Laplace (lien avec l'impédance complexe)
- 3 proba à connaître : 4/ Calculer P( X soit compris entre m - 3sigma et m + 3sigma)
- Synthèse sur les 3 probabilités à connaître
- 2/Déterminer h tel que P( X soit compris entre 75 - h et 75 + h)
- 1/ calculer P( X soit compris entre 74,4 et 75,6)
- Définition de l'original d'un signal avec la transformée en Z
- d. Calculer la proba d'être compris entre 1 et 3
- une pédagogie liée aux erreurs mathématiques
- Partage du cercle en 4 : découverte de l'angle pi/2
- Ex2 : quelle est la mesure en radian de la partie colorée?
- Ex1 : quelle est la mesure en radian de la partie colorée?
- Synthèse sur les partages du cercle en 2, 4 et 8 parties égales.
- Partage du cercle en 6 : découverte de l'angle pi/3
- trouver les valeurs des portions colorées (famille de pi/3)
- Ex2 : quelle est la mesure en radian de la partie colorée?
- Ex1 : quelle est la mesure en radian de la partie colorée?
- Une autre construction importante pour partager un cercle en 6.
- Synthèse : les étapes de construction pour partager un cercle en 6
- Comment partager une cercle en 12 facilement ?
- Synthèse : les étapes de construction pour partager un cercle en 12
- Synthèse sur les différentes familles de base pour les angles remarquables
- Définition du sens trigonométrique
- Placer sur le cercle trigonométrique : 3 pi
- Placer sur le cercle trigonométrique : - 11 pi/6
- Placer sur le cercle trigonométrique : - 5 pi/6
- Placer sur le cercle trigonométrique : 3 pi/4
- Placer sur le cercle trigonométrique : - pi/2
- Placer sur le cercle trigonométrique : rappel du partage du cercle
- Placer sur le cercle trigonométrique : 4 pi/3
- Placer sur le cercle trigonométrique : 4 pi
- Placer sur le cercle trigonométrique : - 19 pi/3
- Placer sur le cercle trigonométrique : 15 pi/4
- Intervalle particulier : cas 1
- Intervalle particulier : cas 2
- Intervalle particulier : cas 3 et intervalle de référence!
- Mesure principale d'un angle sur le cercle trigonométrique
- donner la mesure principale de -9pi
- donner la mesure principale de 13pi/6
- donner la mesure principale de -10pi/3
- donner la mesure principale de 7pi/4
- donner la mesure principale de 5pi/2
- Donner la mesure principale de l'angle coloré
- c. Calculer la proba d'être supérieur ou égal à 2
- Espérance et variance pour des variables indépendantes du type : X+Y ; X-Y ; aX+b
- Calcul de l'écart-type de X+Y, avec X et Y indépendantes
- Calcul de l'espérance et la variance pour la variable : 5X +1
- Calcul de l'espérance et la variance pour la variable : X - Y
- Calcul de l'espérance et la variance pour la variable : X +Y
- Propriété d'unicité de l'original d'un signal avec la transformée en Z
- Application : quelle fonction a pour transformée en Z : z/(z - 1) ?
- quelle fonction a pour transformée en Z : X(z) = 1 ?
- Déterminer l'original de Y(z) = 1/(z + 1) (partie 2 : application des formules)
- Déterminer l'original de Y(z) = 1/(z + 1) (partie 1 : recherche des formules en jeu)
- Quelle fonction a pour transformée en Z : X(z) = 5z/(z - 2) + 4z/(z +4)?
- quelle fonction a pour transformée en Z : X(z) = 4 - 3z/(z - 1) ?
- quelle fonction a pour transformée en Z : Y(z) = 2z/(z - 1)^2 ?
- quelle fonction a pour transformée en Z : Y(z) = z/(z +1) ?
- Méthode pour trouver l'original d'un élément du type : Y(z) = 1/(z + 1)
- Déterminer l'original de X(z) = 4/(z - 1)^2
- Ex : 3/ En déduire l'original y(n)
- Ex : 2/ b) Donner l'original de 1/(z - 1)
- Ex : 2/ a) Donner l'original de 1/z
- Ex : 1/ Déterminer a et b tel que : 1/(z(z - 1)) = a/z + b/(z - 1) (B) identification
- Ex : 1/ Déterminer a et b tel que : 1/(z(z - 1)) = a/z + b/(z - 1) (A)réduire au même dénominateur
- Schéma pour comprendre comment résoudre une équation récurrente avec la transformée en Z
- Ex : 1/ Montrer que (Zx)(z) = z/((z+2)(z -0,5)) : a)transformation de l'éq. avec la TDZ
- Ex : 1/ Montrer que (Zx)(z) = z/((z+2)(z -0,5)) : b) Isoler (Zx)(z)
- Ex : 1/ Montrer que (Zx)(z) = z/((z+2)(z -0,5)) : c) trouver la forme demandée
- Avec une fonction de transfert : 2.B. en déduire y(n)
- Avec une fonction de transfert : 2A. Montrer Y(z) se décompose (b) simpliification
- Avec une fonction de transfert : 2A. Montrer Y(z) se décompose (a)réduction au même dénominateur
- Avec une fonction de transfert : 1C. Montrer que y(n)= ... (partie 2)
- Avec une fonction de transfert : 1C. Montrer que y(n)= ... (partie 1)
- Avec une fonction de transfert : 1B. En déduire que 51Y(z) - 49z^-1 Y(z) = 2X(z) + 2z^-1X(z)
- Avec une fonction de transfert : 1.A/ Montrer que F(z) = 2(z^-1 + 1)/(51 - 49z^-1)
- Ex : 3. Déterminer l'original -(2) conclusion
- Ex : 3. Déterminer l'original -(1) transformation de l'expression
- Ex : 2. Déterminer A et B tel que (Zx)(z) =A/(z+2) + B/(z -0,5) : b) identification et résolution
- Ex : 2. Déterminer A et B tel que (Zx)(z) =A/(z+2) + B/(z -0,5) : a)réduire au même dénominateur
- Formule pour calculer une probabilité du type P(X = k) avec une loi binomiale
- Définition : schéma de Bernouilli.
- Exemple d'une épreuve de Bernouilli
- Ex : 1/ Justifier la loi suivie par X. Préciser l'espérance et l'écart-type
- Ex : 2/ Calculer P(X = 25)
- Ex : 3/ Calculer la proba. que X soit compris entre 24 et 26
- Ex : 4/ Calculer P(Y inférieur à 26)
- Ex : 5/ Calculer la proba. que Y soit compris entre 24 et 26
- Théorème d'approximation d'une loi binomiale par une loi normale
- c/ Donner la proba. d'avoir moins de 50 rondelles non conformes
- b) préciser l'espérance et l'écart-type de la loi normale
- a) Justifier que X suit une loi binomiale et préciser ses paramètres
- a. Calculer la proba d'être exactement en 1
- b. Calculer la proba d'être inférieur strictement à 2
- Th : loi suivie par la somme de 2 variables indépendantes suivant des lois normales
- d/ avec d'autres écart-types, le réglage est-il correct?
- c/ Le réglage est-il correct?
- B) Calculer la proba d'être entre 4,8 et 5,2
- A) déterminer la loi suivie par Z = X + Y
- Théorème de la limite centrée
- Ex: déterminer la loi approchant M400
- Synthèse sur cos et sin d'un angle et une propriété importante
- Propriété de linéarité de la transformée en Z.
- quelle est la transformée en Z de s(n) = 2n - 3 ?
- En appliquant la TEZ à x(n)=4y(n)+e(n), exprimer X(z) en fct de Y(z)
- Explication de la formule : L(f(t) exp( -at) U(t)) = F(p + a)
- Une autre rédaction pour trouver la TDL de g(t) = t^3 exp(2t) U(t)
- application : donner la transformée de Laplace de g(t) = t^3 exp(2t) U(t)
- Quelle est la transformée de Laplace de h(t) = cos(3t) exp(2t) U(t) ?
- Quelle est la transformée de Laplace de g(t) = 2t exp(t) U(t) ?
- Règle 1 : a/b = (a*c)/(b*c) : Application numérique
- Avec la règle 1, Transformer la fraction 14/35
- Avec la règle 1, Transformer la fraction 4
- Avec la règle 1, Transformer la fraction 4/3
- Avec la règle 1, Transformer les fractions 5/2 ; 1/3 ; 2/7
- Règle 1 : a/b = (a*c)/(b*c) : Application algébrique : a)faire apparaitre (x+1)(x-2) au déno
- Règle 1 : a/b = (a*c)/(b*c) : Application algébrique : b)faire apparaitre (x+1)^2 au déno
- Transformer 7/(2p + 1) en 7(2p - 1)/...
- Transformer 5/(x + 2) en ... /(x + 2)(x + 3)
- Transformer 4/x en ... /x^2
- Transformer 5 en ..../(x + 1) et en (5x - 10)/ ...
- Règle 2 : (a*c)/(b*c) = a/b : Interprétation géométrique
- Règle 2 : (a*c)/(b*c) = a/b : Application numérique
- Mettre sous forme irréductible la fraction : 104/84
- Mettre sous forme irréductible la fraction : 27/24
- Mettre sous forme irréductible la fraction : 6/18
- Mettre sous forme irréductible la fraction : 42/36
- Règle 2 : (a*c)/(b*c) = a/b : Application algébrique
- Simplifier l'expression : (2p+6)/(p+3)^2
- Simplifier l'expression : (3x - 3)/ ((x+2)(x-1))
- Simplifier l'expression : (z^2 - z)/ (z(z - 2))
- Règle 3 : a/b + c/b = (a + c)/b : Interprétation géométrique
- Règle 3 : a/b + c/b = (a + c)/b : cas numérique
- Règle 4 : a + b/c = (ac + b)/c : Interprétation géométrique
- Règle 4 : a + b/c = (ac + b)/c : cas numérique
- Règle 5 : a/b + c/d = (ad + cb)/(bd) : interprétation géométrique
- Règle 5 : a/b + c/d = (ad + cb)/(bd) : cas numérique
- Mettre sous forme irréductible : G = - 2/3 + 11/6 - 5/18
- Mettre sous forme irréductible : F = 5/3 + 3/4 - 1
- Mettre sous forme irréductible : E = -2/5 + 3
- Mettre sous forme irréductible : D = 17/8+ (-3/4)
- Mettre sous forme irréductible : C = 5/3 - 7/4
- Mettre sous forme irréductible : B = 2 + 2/9
- Mettre sous forme irréductible : A = 7/6 + 5/6
- Règle 3 : a/b + c/b = (a + c)/b : cas algébrique
- Règle 4 : a + b/c = (ac + b)/c : cas algébrique
- Règle 5 : a/b + c/d = (ad + cb)/(bd) : cas algébrique
- réduction au même dénominateur d'une fraction en z : b) réduction
- réduction au même dénominateur d'une fraction en z : a) simplification
- réduire au même dénominateur : 1/p - 1/(p +20)
- Réduire : 5x/(2x + 2) - 10x/(4x - 4)
- réduire: 5/(x + 1) + 3/(2 - x)
- Réduire : 4/x - 2
- Réduire au même dénominateur : e)2/x - 4/x^2
- Réduire au même dénominateur : d) (2x + 1)/x - 2x/(x + 4)
- Réduire au même dénominateur : c) 5/x + 3/(2x + 1)
- Réduire au même dénominateur : b) (-2x + 3)/(x - 1) - 4
- Réduire au même dénominateur : a) 2x/(1- 5x) - (4x -3)/(1 - 5x)
- Règle 1 : a/b = (a*c)/(b*c) : Interprétation géométrique
- Définition d'une fraction
- Comment représenter les 15/6 d'une barre ?
- Comment représenter la fraction 2/3 et 3/4 ?
- Carré d'un nombre : 1/ cas numérique
- Carré d'un nombre : 2/ Comprendre qui est "a au carré"
- Carré d'un nombre : 3/ a) Comprendre à quoi correspond 2x + 1 au carré
- Carré d'un nombre : 3/ b) Attention à ce que vous dites ...
- Traduire des expressions mathématiques en phrases (partie2)
- Traduire des expressions mathématiques en phrases (partie1)
- Traduire des phrases en expressions mathématiques contenant le mot "carré" (partie2)
- Traduire des phrases en expressions mathématiques contenant le mot "carré" (partie1)
- Comprendre géométriquement ce que représentent les famille de x, de x^2, de x^3
- Trouver les différentes familles dans l'expression 3x^2 + 5x + 2
- Définition de "réduire"
- réduire 3 expressions
- Remarque : peut on regrouper des éléments du type a^2 et x^2 ensemble?
- réduire des expressions qui contiendrait les éléments du même type
- Comprendre géométrique la formule : k(a+b) = ka + kb
- Définition : développer une expression
- développer D = 3x + 2 - 2(x + 1)
- développer C = x(x + 2) - 3x
- développer B = 5(3 - d) - 3(7 - d)
- développer A = 4(2x + 3)
- Application : développer A = -2 (p + 3)
- Définition : factoriser une expression
- factoriser C = 4(x+3)(x-2) +5x(x+3) : b) réduire au maximum
- factoriser C = 4(x+3)(x-2) +5x(x+3) : a) mise en facteur
- factoriser B = (p +1)(p +2) - 3(p +1)
- factoriser A = p^2 + 5p
- Application : factoriser B = 4(a +2) + 4(a + 1)
- Formule de la double distributivité : a) interprétation géométrique
- Formule de la double distributivité : b) utilisation des "flèches" comme méthode
- Application de la formule de double distributivité : développer A = (x + 2)(x + 3)
- développer (y + 4)(y + 5)
- développer (4p + 1 )(2 + p)
- développer (x + 2)(x + 9)
- Double distributivité et la règle des signes : que devient la formule (a+b)(c - d)?
- Double distributivité et la règle des signes : que devient la formule (a-b)(c + d)?
- Double distributivité et la règle des signes : que devient la formule (a-b)(c -d)?
- développer C = (3 + 2p)(1 - p)
- développer B = (1 - 2y)(3 - 5y)
- développer A = (2x - 1)(3 + x)
- Map de synthèse sur parité, périodicité et intégrale : a) si f ni paire ni impaire
- Map de synthèse sur parité, périodicité et intégrale : b) si f paire
- Map de synthèse sur parité, périodicité et intégrale : c) si f impaire
- Rayon de convergence d'une série entière
- Signaux discrets de référence : a/ L'échelon unité discret noté e
- Signaux discret de référence : b/ la rampe discrète notée r
- Signaux discret de référence : c/ le signal carré discret noté c
- Signaux discret de référence : d/ le signal exponentiel discret
- Signaux discret de référence : e/ le signal impulsion unité discrète
- tracer x(n) = 5n - 2
- Traduire le signal y(n) = 3n^2 -6n + 1 en fonction des signaux usuels
- Traduire le signal x(n) = 5n - 2 en fonction des signaux usuels
- Définition d'un signal retardé de n0 unités : x(n - n0)
- Application : à partir du tracé de x(n), tracer y(n) = x(n - 2)
- Généralisation : quelle transformation permet de passer de x(n) à y(n) = x(n - n0)?
- Ex: 2/ tracer x(n-3) sachant que x(n)= 4r(n) - 3e(n)
- Ex: 1/ tracer x(n) = 4r(n) - 3 e(n)
- tracer d(n - 3)
- tracer e(n - 2)
- 2/ quelle transformation géométrique permet de passer de r(n) à x(n) = r(n - 1)?
- 1/ tracer x(n) = r(n - 1)
- Définition : signal avancé de n0 unités : x(n + n0)
- Comprendre la différence entre un signal "avancé" et "retardé" de n0 unités
- Ex : 2/Quelle transformation géométrique permet de passer de x(n) à t(n)=r(n+2)?
- Ex : 1/ Tracer t(n) = r(n + 2)
- 2. Quelle transformation géométrique permet de passer de x(n) à y(n)=x(n+1)?
- 1. Tracer y(n) = x(n + 1) à partir du graphe du signal x
- Introduction : Pourquoi a-t-on introduit la transformée en Z?
- Définition de la transformée en Z
- Tableau des transformées en Z des signaux de référence
- Application : quelle est la transformée en Z de f(n) = 2^n ?
- Définition d'une série entière
- Exemples de séries entières
- Règle 8 : (a/b)/(c/d) = (a/b) * (d/c) : cas algébrique : calculer 2/(x-1) / ((x+2)/6)
- Règle 6 : a/b * c/d = (ac)/(bd) : Interprétation géométrique
- Règle 6 : a/b * c/d = (ac)/(bd) : cas numérique
- Simplifier : D = 15/(-39) * (-3)
- Simplifier : A = 5/7 * 11/10
- Simplifier : B = - 2* 4/7
- Simplifier : C = -6/5 * 3/8 * (-10/9)
- Simplifier : E = 15/14 * 28/25
- Règle 6 : a/b * c/d = (ac)/(bd) : cas algébrique
- Simplifier au maximum : (z^2/(z - 2)) * 4/z
- Simplifier au maximum : ((3x - 3)/(x + 2)) * (x/(x - 1))
- Simplifier au maximum : 4 * x/(x + 1)
- Simplifier au maximum : (2/(p + 3)) * ((p + 6)/(p + 3))
- Règle 7 : 1/(a/b) = b/a : Interprétation géométrique
- Règle 7 : 1/(a/b) = b/a : cas numérique : a) calculer 1/(1/3)
- Règle 7 : 1/(a/b) = b/a : cas numérique : b) quel est l'inverse de 3/4 ?
- Ex : calculer A = 1/(1/6) ; B = 1/(-5/3) et C = - 1/(2/(-3))
- donner l'inverse des nombres suivants...
- Règle 7 : 1/(a/b) = b/a : cas algébrique
- transformer 1/((x+5)/6)
- transformer 1/(1/(2p+4))
- Que donne le développement de (a + b)(c + d + e) ?
- Application développer A = (x - 2)(2x^2 - 3x + 1) : 1/ double distributivité
- Application développer A = (x - 2)(2x^2 - 3x + 1) : 2/ réduire
- développer (x - 2)(ax^2 + bx + c) : 2/ réduire
- développer (x - 2)(ax^2 + bx + c) : 1/ double distributivité
- développer (x + 1)(ax^2 + bx + c) : 2/ réduire
- développer (x + 1)(ax^2 + bx + c) : 1/ double distributivité
- Laplace pour résoudre une équation différentielle : a) Transformée de Laplace appliquée à l'équation
- Laplace pour résoudre une équation différentielle : b) isoler Y(p)
- Laplace pour résoudre une équation différentielle : c) déterminer l'original de Y(p)
- Dans un circuit RC : 2. Montrer que V(p) = 2/(p(p + 3))
- Dans un circuit RC : 1.B/ exprimer la transformée de Laplace E(p) de e(t)
- Dans un circuit RC : 1.A/ tracer la courbe de e(t) = 2 U(t)
- Dans un circuit RC : 3. Vérifier que V(p) = 2/(3p) - 2/(3(p + 3))
- Ex avec une fonction de transfert : c) recherche de l'original v(t)
- Ex avec une fonction de transfert : c) transformation de V(p)
- Ex avec une fonction de transfert : b) identification
- Ex avec une fonction de transfert : b) réduction au même dénominateur
- Ex avec une fonction de transfert : a) définir E(p)
- Ex avec une fonction de transfert : a) définir S(p)
- Dans un circuit RC : 4. b) recherche de l'original
- Dans un circuit RC : 4. a)Transformation de V(p)
- Règle 8 : (a/b)/(c/d) = (a/b) * (d/c) : Interprétation géométrique
- Règle 8 : (a/b)/(c/d) = (a/b) * (d/c) : cas numérique : calculer (7/4)/(3/2)
- simplifier E = (-9/4)/(-6/5)
- simplifier D = (-7/4)/-21
- simplifier C = (3/4)/5
- simplifier B = 3/(4/5)
- simplifier A = (5/9)/(-2/3)
- Application : quelle est la transformée en Z de x(n) = (-1)^n ?
- 2. Interprétation graphique de l'intégrale pour une fonction positive : c)l'intégrale
- Tableau donnant les différentes limites d'une somme de deux fonctions
- Calcul de 3 limites pour la somme de 2 fonctions
- A partir des graphes, donner les valeurs de limites en +∞ou - ∞
- A partir des graphes, donner les valeurs de 3 limites en un point
- Définition de la limite d 'une fonction
- Définition de 'tendre vers'
- Démonstration : trouver la forme des solutions des équa. diff. SANS 2nd membre
- Démonstration de la formule d'intégration par partie (abrégé IPP)
- IPP pour l'intégrale de f(t) = t cos(nt) entre 0 et pi : b) application de la formule et calcul
- IPP pour l'intégrale de f(t) = t cos(nt) entre 0 et pi : a) le schéma d'intégration
- IPP pour l'intégrale de f(t) = t cos(2t) entre 0 et pi/2 : b) application de la formule et calcul
- IPP pour l'intégrale de f(t) = t cos(2t) entre 0 et pi/2 : a) le schéma d'intégration
- IPP pour l'intégrale de f(t) = t exp(t) entre 0 et 1 : b) application de la formule et calcul
- IPP pour l'intégrale de f(t) = t exp(t) entre 0 et 1 : a) le schéma d'intégration
- IPP pour l'intégrale de f(x) = x ln(x) entre 1 et e : b) application de la formule et calcul
- IPP pour l'intégrale de f(x) = x ln(x) entre 1 et e : a) le schéma d'intégration
- Introduction sur la notion de série
- Théorie : b)résoudre une équa. diff du 2nd ordre AVEC second membre
- Résoudre x' '(t)- 4x'(t) +3x(t) = -3t²+2t : c)solutions générales
- Résoudre x' '(t)- 4x'(t) +3x(t) = -3t²+2t : b)solution particulière- (3) système
- Résoudre x' '(t)- 4x'(t) +3x(t) = -3t²+2t : b)solution particulière- (2) Identification
- Résoudre x' '(t)- 4x'(t) +3x(t) = -3t²+2t : b)solution particulière-(1) Dérivées successives
- Résoudre x' '(t)- 4x'(t) +3x(t) = -3t²+2t : a)résolution de (E0)
- Résoudre x' '(t) -2x'(t) + 5x(t) = 5 cos(t) : a)résoudre (E0)
- Résoudre x' '(t)- 4x'(t) +3x(t) = -3t²+2t : d)avec les 2 conditions initiales
- Résoudre x' '(t) -2x'(t) + 5x(t) = 5 cos(t) : b)solution particulière
- Résoudre x' '(t) -2x'(t) + 5x(t) = 5 cos(t) : c)solutions générales de (E)
- Dérivées de fonctions usuelles
- Dérivée de x^n
- 2. Interprétation graphique de l'intégrale pour une fonction POSITIVE : b)expression de f
- 2. Interprétation graphique de l'intégrale pour une fonction positive : a)calcul de l'aire
- 1. Interprétation graphique de l'intégrale pour une fonction POSITIVE
- Théorème du retard avec la transformée en Z
- Application : f) 3- Donner l'expression de s(t) pour t supérieur à 1
- Voca : Etre solution particulière
- Solution particulière : b) dérivée de h
- Solution particulière : a) traduction de l'énoncé
- Lien avec la physique : b/ déterminer les valeurs de a, b et c
- Lien avec la physique : a) comment s'appelle cette équation ?
- Ex2 : b/ Déterminer les valeurs de a, b, c et d(x)
- Ex2 : a/ Déterminer l'équa. diff. SANS second membre
- Ex1 : c) Solution particulière - (2) Vérification
- Ex1 : c) Solution particulière - (1) calcul des dérivées successives
- Ex1 : b/ Déterminer les valeurs de a, b et c
- Ex1 : a/ Déterminer l'éq. diff. SANS second membre
- Solution particulière : c) dérivée seconde de h
- Solution particulière : d) remplacement dans l'équation et vérification
- Trouver g solution particulière d'une équa. diff. du 2nd ordre : a)dérivées successives
- Trouver g solution particulière d'une équa. diff. du 2nd ordre : b) remplacement
- Trouver g solution particulière d'une équa. diff. du 2nd ordre : c) identification
- Trouver g solution particulière d'une équa. diff. du 2nd ordre : d) résoudre le système
- Voca : définition d'une équa. diff. du 2nd ordre SANS second membre
- Voca : résoudre une équa. diff.
- Voca : définition d'une équa. diff. du 2nd ordre AVEC second membre
- Propriété sur le produit de fonctions et la parité
- f(t) = tcos(2t) : b)calcul de l'intégrale de f sur [- pi; pi ]
- f(t) = tcos(2t) : a)montrer que f est impaire (2nde méthode)
- f(t) = tcos(2t) : a)montrer que f est impaire (1ière méthode)
- Dire si les fonctions sont paires ou impaires
- Intégrale d'une fonction impaire sur un intervalle centré